题目内容
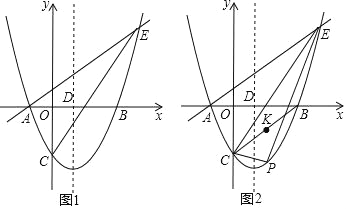
【题目】如图,在平面直角坐标系中,抛物线y=x2﹣2x﹣3与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,对称轴x轴交于点D,点E(4,n)在抛物线上.
(1)求直线AE的解析式;
(2)连接CB,点K是线段CB的中点,点M是y轴上的一点,点P为直线CE下方抛物线上的一点,连接PC,PE,当△PCE的面积最大时,求KM+PM的最小值;
(3)点G是线段CE的中点,将抛物线y=x2﹣2x﹣3沿x轴正方向平移得到新抛物线y′,y′经过点D,y′的顶点为点F,在新抛物线y′的对称轴上,是否存在一点Q,使得△FGQ为等腰三角形?若存在,直接写出点Q的坐标;若不存在,请说明理由.
【答案】(1)直线AE的解析式为y=x+1;(2)当△PCE的面积最大时,KM+PM的最小值为![]() ;(3)点Q的坐标为(3,-4-
;(3)点Q的坐标为(3,-4-![]() )或(3,-4+
)或(3,-4+![]() )或(3,6)或(3,
)或(3,6)或(3,![]() ).
).
【解析】
(1)利用二次函数图象上点的坐标特征可求出点A、B、E的坐标,根据点A、E的坐标,利用待定系数法即可求出直线AE的解析式;
(2)利用二次函数图象上点的坐标特征可求出点C的坐标,根据点C、E的坐标,利用待定系数法即可求出直线CE的解析式,过点P作PP′∥y轴,交直线CE于点P′,作点K关于y轴对称点K′,连接PK′交y轴于点M,此时PM+KM取最小值PK′,设点P的坐标为(x,x2﹣2x﹣3),则点P′的坐标为(x,2x﹣3),PP′=﹣x2+4x,根据三角形面积公式可得出S△PCE=﹣2x2+8x,配方后可得出:当x=2时,△PCE的面积取最大值,此时点P的坐标为(2,﹣3),由点B、C的坐标可得出点K、K′的坐标,再利用两点间的距离公式可求出当△PCE的面积最大时KM+PM的最小值;
(3)根据平移的性质结合平移后的抛物线过点D可求出平移后抛物线的解析式,进而可求出其顶点F的坐标,由点C、E的坐标可求出点G的坐标,设点Q的坐标为(3,a),则GF=![]() =
=![]() ,FQ=|a+4|,GQ=
,FQ=|a+4|,GQ=![]() =
=![]() ,根据等腰三角形的性质分GF=FQ、GF=GQ、FQ=GQ三种情况求出a的值,此题得解.
,根据等腰三角形的性质分GF=FQ、GF=GQ、FQ=GQ三种情况求出a的值,此题得解.
(1)当y=0时,有x2﹣2x﹣3=0,解得:x1=﹣1,x2=3,∴A(﹣1,0),B(3,0).
当x=4时,y=x2﹣2x﹣3=5,∴E(4,5).
设直线AE的解析式为y=kx+b(k≠0),将A(﹣1,0)、E(4,5)代入y=kx+b中,得:![]() ,解得:
,解得:![]() ,∴直线AE的解析式为y=x+1.
,∴直线AE的解析式为y=x+1.
(2)当x=0时,y=x2﹣2x﹣3=﹣3,∴C(0,﹣3),设直线CE的解析式为y=mx﹣3(m≠0),将点E(4,5)代入y=mx﹣3中,得:
4m﹣3=5,解得:m=2,∴直线CE的解析式为y=2x﹣3.
在图2中,过点P作PP′∥y轴,交直线CE于点P′,作点K关于y轴对称点K′,连接PK′交y轴于点M,此时PM+KM取最小值PK′.
设点P的坐标为(x,x2﹣2x﹣3),则点P′的坐标为(x,2x﹣3),PP′=﹣x2+4x,∴S△PCE=![]() PP′(xE﹣xC)=﹣2x2+8x=﹣2(x﹣2)2+8,∴当x=2时,△PCE的面积取最大值,此时点P的坐标为(2,﹣3).
PP′(xE﹣xC)=﹣2x2+8x=﹣2(x﹣2)2+8,∴当x=2时,△PCE的面积取最大值,此时点P的坐标为(2,﹣3).
∵B(3,0),C(0,﹣3),K是线段CB的中点,∴K(![]() ,﹣
,﹣![]() ),K′(﹣
),K′(﹣![]() ,﹣
,﹣![]() ),∴PK′=
),∴PK′=![]() =
=![]() ,∴当△PCE的面积最大时,KM+PM的最小值为
,∴当△PCE的面积最大时,KM+PM的最小值为![]() .
.
(3)设平移后的抛物线的解析式为y=(x﹣t)2﹣2(x﹣t)﹣3(t>0).
∵平移后的抛物线过点D(1,0),∴(1﹣t)2﹣2(1﹣t)﹣3=0,解得:t1=2,t2=﹣2(舍去),∴平移后抛物线的解析式为y=(x﹣2)2﹣2(x﹣2)﹣3=x2﹣6x+5=(x﹣3)2﹣4,∴F(3,﹣4).
∵C(0,﹣3),E(4,5),点G是线段CE的中点,∴G(2,1).
设点Q的坐标为(3,a),则GF=![]() =
=![]() ,FQ=|a+4|,GQ=
,FQ=|a+4|,GQ=![]() =
=![]() .
.
∵△FGQ为等腰三角形,∴分三种情况.
①当GF=FQ时,有![]() =|a+4|,解得:a1=
=|a+4|,解得:a1=![]() ﹣4,a2=﹣
﹣4,a2=﹣![]() ﹣4,∴点Q(3,
﹣4,∴点Q(3,![]() ﹣4)或(3,﹣
﹣4)或(3,﹣![]() ﹣4);
﹣4);
②当GF=GQ时,有![]() =
=![]() ,解得:a3=6,a4=﹣4(舍去),∴点Q(3,6);
,解得:a3=6,a4=﹣4(舍去),∴点Q(3,6);
③当FQ=GQ时,有|a+4|=![]() ,解得:a=﹣
,解得:a=﹣![]() ,∴点Q(3,﹣
,∴点Q(3,﹣![]() ).
).
综上所述:在新抛物线y′的对称轴上,存在一点Q,使得△FGQ为等腰三角形,点Q的坐标为(3,![]() )或(3,
)或(3,![]() )或(3,6)或(3,
)或(3,6)或(3,![]() ).
).