题目内容
如图,在Rt△ABC中,∠A=30°,BC=1,点D,E分别是直角边BC,AC的中点,则DE的长为( )

A. 1 B. 2 C.  D. 1+
D. 1+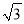
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案(问题提出)
我们借助学习“图形的判定”获得的经验与方法对“平行四边形的判定”进一步探究.

(初步思考)
在一个四边形中,我们把“一组对边平行、一组对边相等、一组对角相等或一条对角线被另一条对角线平分”称为一个条件.如图1,四边形ABCD中,我们用符号语言表示出所有的8个条件:
①AB=CD; | ②AD=BC; | ③AB∥CD; | ④AD∥BC; |
⑤∠BAD=∠BCD; | ⑥∠ABC=∠ADC; | ⑦OA=OC; | ⑧OB=OD. |
那么满足2个条件的四边形是不是平行四边形呢?
(深入探究)
小莉所在学习小组进行了研究,她们认为2个条件可分为以下六种类型:
Ⅰ关于对边的2个条件;Ⅱ关于对角的2个条件;
Ⅲ关于对角线的2个条件;Ⅳ关于边的条件与角的条件各1个;
Ⅴ关于边的条件与对角线的条件各1个;Ⅵ关于角的条件与对角线的条件各1个.
(1)小明认为“Ⅰ关于对边的2个条件”可分为“①②,③④,①③,①④”共4种不同种类的情形.请你仿照小明的叙述对其它五种类型进一步分类.
(2)小红认为有4种情形是平行四边形的判定依据.请你写出其它的三个判定定理.
定义:两组对边分别平行的四边形是平行四边形;
定理1:
定理2: ;
定理3: .
(3)小刚认为除了4个判定依据外,还存在一些真命题,他写出了其中的1个,请证明这个真命题,并仿照他的格式写出其它真命题(无需证明):
真命题1:四边形ABCD中,若∠BAD=∠BCD,∠ABC=∠ADC,则四边形ABCD是平行四边形.
(4)小亮认为,还存在一些假命题,他写出了其中的1个,并举反例进行了说明,请你仿照小亮的格式写出其它假命题并举反例进行说明.
假命题1:四边形ABCD中,若AB=CD,AD∥BC,则四边形ABCD不一定是平行四边形.
反例说明:如图2,四边形ABCD中,AB=CD,AD∥BC,显然四边形ABCD不是平行四边形.


 的计算结果为( )
的计算结果为( ) B.
B.  C.
C.  D.
D. 

 B. 3
B. 3

 的值.
的值.
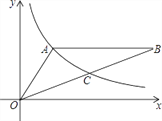
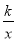 (x>0)经过△OAB的顶点A和OB的中点C,AB∥x轴,点A的坐标为(2,3),求△OAC的面积是________.
(x>0)经过△OAB的顶点A和OB的中点C,AB∥x轴,点A的坐标为(2,3),求△OAC的面积是________.