题目内容
在求1+2+22+…+22010+22011的值时,可设S=1+2+22+…+22010+220①,则2S=2+22+23+…+22011+22012②,再由②-①得,S=22012-1.利用上述方法求1+3+32+…+32010+32011的值是
- A.32012-1
- B.32012-2
- C.
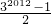
- D.
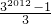
C
分析:可设S=1+3+32+…+32010+32011,两边都乘以3后,相减,再除以S的系数可得结果.
解答:S=1+3+32+…+32010+32011①,
①×3得3S=3+32+…+32011+32012②,
②-①得2S=32012-1,
S=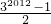 .
.
故选C.
点评:考查数字的变化规律;关键是理解题意,利用类比的思想解决问题.
分析:可设S=1+3+32+…+32010+32011,两边都乘以3后,相减,再除以S的系数可得结果.
解答:S=1+3+32+…+32010+32011①,
①×3得3S=3+32+…+32011+32012②,
②-①得2S=32012-1,
S=
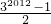 .
.故选C.
点评:考查数字的变化规律;关键是理解题意,利用类比的思想解决问题.

练习册系列答案
相关题目