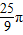题目内容
若正方形内切圆的面积πcm2，则它的外接圆的面积是（ ）cm2．
| A、2π | ||
B、
| ||
C、
| ||
D、
|
分析：根据题意画出图形，连接OB、OC过O作OE⊥BC，再根据正方形的性质求出∠BOC的度数；进而由垂径定理求出BE的长，从而由勾股定理求出大圆的半径即可．
解答：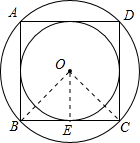
解：如图所示，连接OB、OC，过O作OE⊥BC；
∵四边形ABCD是正方形，
∴∠BOC=
=90°，
∵OB=OC，OE⊥BC，
∴∠BOE=
=
=45°，
∴BE=OE；
∵正方形ABCD的内切圆面积为πcm2，
∴OE=BE=1，
∴OB=
=
=
cm，
∴S外接圆=π（OB）2=π（
）2=2πcm2．
故选A．
解：如图所示，连接OB、OC，过O作OE⊥BC；∵四边形ABCD是正方形，
∴∠BOC=
| 4 |
| 360° |
∵OB=OC，OE⊥BC，
∴∠BOE=
| ∠BOC |
| 2 |
| 90° |
| 2 |
∴BE=OE；
∵正方形ABCD的内切圆面积为πcm2，
∴OE=BE=1，
∴OB=
| OE2+BE2 |
| 12+12 |
| 2 |
∴S外接圆=π（OB）2=π（
| 2 |
故选A．
点评：此题主要考查正多边形的计算问题，属于常规题．
练习册系列答案
相关题目
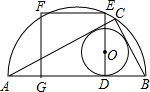如图，AB为半圆的直径，C是半圆弧上一点，正方形DEFG的一边DG在直径AB上，另一边DE过△ABC的内切圆圆心O，且点E在半圆弧上．若正方形DEFG的面积为100，且△ABC的内切圆半径r=4，则半圆的直径AB=
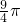
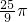
π
π
π
