题目内容
(2005•黑龙江)如图所示,在平面直角坐标系中,Rt△ABC的斜边AB在x轴上,AB=25,顶点C在y轴的负半轴上,tan∠ACO= ,点P在线段OC上,且PO、PC的长(PO<PC)是关于x的方程x2-(2k+4)x+8k=0的两根.
,点P在线段OC上,且PO、PC的长(PO<PC)是关于x的方程x2-(2k+4)x+8k=0的两根.(1)求AC、BC的值;
(2)求P点坐标;
(3)在x轴上是否存在点Q,使以点A、C、P、Q为顶点的四边形是梯形?若存在,请直接写出直线PQ的解析式;若不存在,请说明理由.

【答案】分析:(1)根据tan∠ABC=- ,可设AC=3a,BC=4a则AB=5a,5a=25,a=5,所以AC=15,BC=20;
,可设AC=3a,BC=4a则AB=5a,5a=25,a=5,所以AC=15,BC=20;
(2)根据面积公式可求得OC=12,因为PO+PC=4+2k=12,所以k=4,根据PO、PC的长(PO<PC)是关于x的方程x2-(2k+4)x+8k=0的两根.可求得PO=4,即P(0,-4);
(3)根据梯形的性质求出点Q的坐标分为两种情况:②AP平行于CQ,②AC平行于PQ,先分别求出AP和AC的解析式yAP=- x-4和yAC=-
x-4和yAC=- x-12,结合两直线平行时,k的值相等,求出对应的Q坐标,结合点P的坐标利用待定系数法可求得直线PQ解析式为:y=-
x-12,结合两直线平行时,k的值相等,求出对应的Q坐标,结合点P的坐标利用待定系数法可求得直线PQ解析式为:y=- x-4或y=-
x-4或y=-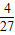 x-4.
x-4.
解答:解:(1)∵∠ACB=90°,CO⊥AB,
∴∠ACO=∠ABC,
∴tan∠ABC=- ,
,
Rt△ABC中,设AC=3a,BC=4a,
则AB=5a,5a=25,
∴a=5,
∴AC=15,BC=20.
(2)∵S△ABC= AC•BC=
AC•BC= OC•AB,
OC•AB,
∴OC=12∴PO+PC=4+2k=12,
∴k=4,
∴方程可化为x2-12x+32=0,解得x1=4,x2=8;∵PO<PC,
∴PO=4,∴P(0,-4).
(3)存在,直线PQ解析式为:y=- x-4或y=-
x-4或y=-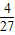 x-4,
x-4,
说明:如果学生有不同于本参考答案的解题方法,只要正确,可参照本评分标准,酌情给分.
点评:主要考查了函数和几何图形的综合运用.解题的关键是会灵活的运用函数图象的性质和交点的意义求出相应的线段的长度或表示线段的长度,再结合具体图形的性质求解.
 ,可设AC=3a,BC=4a则AB=5a,5a=25,a=5,所以AC=15,BC=20;
,可设AC=3a,BC=4a则AB=5a,5a=25,a=5,所以AC=15,BC=20;(2)根据面积公式可求得OC=12,因为PO+PC=4+2k=12,所以k=4,根据PO、PC的长(PO<PC)是关于x的方程x2-(2k+4)x+8k=0的两根.可求得PO=4,即P(0,-4);
(3)根据梯形的性质求出点Q的坐标分为两种情况:②AP平行于CQ,②AC平行于PQ,先分别求出AP和AC的解析式yAP=-
 x-4和yAC=-
x-4和yAC=- x-12,结合两直线平行时,k的值相等,求出对应的Q坐标,结合点P的坐标利用待定系数法可求得直线PQ解析式为:y=-
x-12,结合两直线平行时,k的值相等,求出对应的Q坐标,结合点P的坐标利用待定系数法可求得直线PQ解析式为:y=- x-4或y=-
x-4或y=-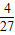 x-4.
x-4.解答:解:(1)∵∠ACB=90°,CO⊥AB,
∴∠ACO=∠ABC,
∴tan∠ABC=-
 ,
,Rt△ABC中,设AC=3a,BC=4a,
则AB=5a,5a=25,
∴a=5,
∴AC=15,BC=20.
(2)∵S△ABC=
 AC•BC=
AC•BC= OC•AB,
OC•AB,∴OC=12∴PO+PC=4+2k=12,
∴k=4,
∴方程可化为x2-12x+32=0,解得x1=4,x2=8;∵PO<PC,
∴PO=4,∴P(0,-4).
(3)存在,直线PQ解析式为:y=-
 x-4或y=-
x-4或y=-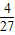 x-4,
x-4,说明:如果学生有不同于本参考答案的解题方法,只要正确,可参照本评分标准,酌情给分.
点评:主要考查了函数和几何图形的综合运用.解题的关键是会灵活的运用函数图象的性质和交点的意义求出相应的线段的长度或表示线段的长度,再结合具体图形的性质求解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,点P在线段OC上,且PO、PC的长(PO<PC)是关于x的方程x2-(2k+4)x+8k=0的两根.
,点P在线段OC上,且PO、PC的长(PO<PC)是关于x的方程x2-(2k+4)x+8k=0的两根.
 轴上,tan∠ABC=
轴上,tan∠ABC= ,点P在线段OC上,且PO、PC的长(PO<PC)是方程x2-12x+27=0的两根.
,点P在线段OC上,且PO、PC的长(PO<PC)是方程x2-12x+27=0的两根. 轴上,tan∠ABC=
轴上,tan∠ABC= ,点P在线段OC上,且PO、PC的长(PO<PC)是方程x2-12x+27=0的两根.
,点P在线段OC上,且PO、PC的长(PO<PC)是方程x2-12x+27=0的两根.