题目内容
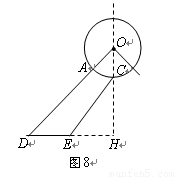
“创意设计”公司员工小王不慎将墨水泼在一张设计图纸上,导致其中部分图形和数据看不清楚(如图所示).已知图纸上的图形是某建筑物横断面的示意图,它是以圆O的半径OC所在的直线为对称轴的轴对称图形,A是OD与圆O的交点.(1)请你帮助小王在图中把图形补画完整;
(2)由于图纸中圆O的半径r的值已看不清楚,根据上述信息(图纸中i=1:0.75是坡面CE的坡度),求r的值.
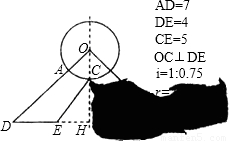
【答案】分析:(1)由图形是关于半径OC所在直线为对称轴的轴对称图形,将图形补画完整.
(2)由坡面CE的坡度求得CH、EH的长,再在△DOH中,运用勾股定理求得圆O的半径r.
解答: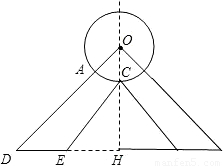 解:(1)补全图形如下:
解:(1)补全图形如下:
(2)解:由已知OC⊥DE,垂足为点H,则∠CHE=90°.
∵i=1:0.75,∴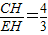 .
.
在Rt△HEC中,EH2+CH2=EC2.
设CH=4k,EH=3k(k>0),
又∵CE=5,得(3k)2+(4k)2=25,解得k=1.
∴EH=3,CH=4.∴DH=DE+EH=7,
OD=OA+AD=r+7,OH=OC+CH=r+4.
在Rt△ODH中,OH2+DH2=OD2,
∴(r+4)2+72=(r+7)2.
解得:r= .
.
点评:此题主要考查学生对坡度坡角的掌握及三角函数、勾股定理的运用能力.
(2)由坡面CE的坡度求得CH、EH的长,再在△DOH中,运用勾股定理求得圆O的半径r.
解答:
 解:(1)补全图形如下:
解:(1)补全图形如下:(2)解:由已知OC⊥DE,垂足为点H,则∠CHE=90°.
∵i=1:0.75,∴
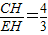 .
.在Rt△HEC中,EH2+CH2=EC2.
设CH=4k,EH=3k(k>0),
又∵CE=5,得(3k)2+(4k)2=25,解得k=1.
∴EH=3,CH=4.∴DH=DE+EH=7,
OD=OA+AD=r+7,OH=OC+CH=r+4.
在Rt△ODH中,OH2+DH2=OD2,
∴(r+4)2+72=(r+7)2.
解得:r=
 .
.点评:此题主要考查学生对坡度坡角的掌握及三角函数、勾股定理的运用能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 称图形,A是OD与圆O的交点.
称图形,A是OD与圆O的交点. 的半径
的半径 所在的直线为对称轴的轴对称图形,
所在的直线为对称轴的轴对称图形,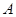 是
是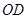 与圆
与圆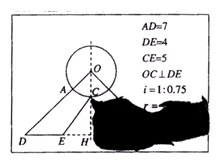

 的值已看不清楚,根据上述信息(图纸中
的值已看不清楚,根据上述信息(图纸中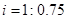 是坡面
是坡面 的坡度),求
的坡度),求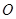 的半径
的半径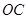 所在的直线为对称轴的轴对称图形,
所在的直线为对称轴的轴对称图形,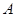 是
是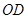 与圆
与圆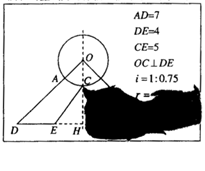

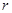 的值已看不清楚,根据上述信息(图纸中
的值已看不清楚,根据上述信息(图纸中 是坡面
是坡面 的坡度),求
的坡度),求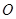 的半径
的半径 所在的直线为对称轴的轴对称图形,
所在的直线为对称轴的轴对称图形,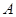 是
是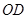 与圆
与圆

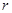 的值已看不清楚,根据上述信息(图纸中
的值已看不清楚,根据上述信息(图纸中 是坡面
是坡面 的坡度),求
的坡度),求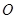 的半径
的半径 所在的直线为对称轴的轴对称图形,
所在的直线为对称轴的轴对称图形,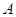 是
是 与圆
与圆
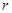 的值已看不清楚,根据上述信息(图纸中
的值已看不清楚,根据上述信息(图纸中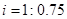 是坡面
是坡面 的坡度),求
的坡度),求