题目内容
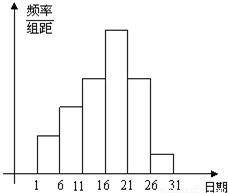
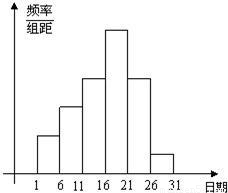
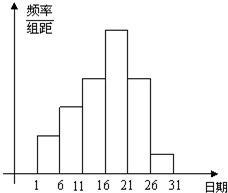
武汉市教育局在中学开展的“创新素质实践行”中,进行了小论文的评比.各校交论文的时间为5月1日至30日,评委会把各校交的论文的件数按5天一组分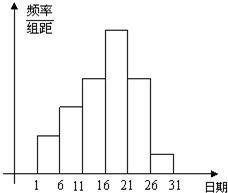 组统计,绘制了频率分布直方图,已知从左至右各长方形的高的比为2:3:4:6:4:1,第二组的频数为18.请回答下列问题:
组统计,绘制了频率分布直方图,已知从左至右各长方形的高的比为2:3:4:6:4:1,第二组的频数为18.请回答下列问题:
(1)本次活动共有多少篇论文参加评比?
(2)哪组上交的论文数量最多有多少篇?
(3)经过评比,第四组和第六组分别有20篇、4篇论文获奖,问这两组哪组获奖率较高?
答:(1)第二组的频率是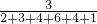 =0.15,
=0.15,
总篇数是18÷0.15=120.
则本次活动共有120篇论文参评;
(2)第四组上交的论文数量最多,有36篇;
(3)第六组获奖率最高.
分析:(1)由题意可知:从左至右各长方形的高的比为2:3:4:6:4:1,则从左到右的各组的频率为0.1、0.15、0.2、0.3、0.2、0.05,又知第二组的频数为18,则总篇数=第二组的频数÷第二组的频率;
(2)由图可以看出第四组的频率组大,则第四组的论文数量最多;
(3)第四组的论文的频数=120×0.3=36篇,第六组的论文的频数=120×0.05=6篇;则第四组的获奖率=20÷36=56%,第六组的获奖率为4÷6=67%;则第六组的获奖率较高.
点评:本题考查频率的意义,虽然题目没有直接告诉频率,但可以求出来;知道了频率、频数即及总数中的任何两个量就可以求第三个量.
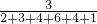 =0.15,
=0.15,总篇数是18÷0.15=120.
则本次活动共有120篇论文参评;
(2)第四组上交的论文数量最多,有36篇;
(3)第六组获奖率最高.
分析:(1)由题意可知:从左至右各长方形的高的比为2:3:4:6:4:1,则从左到右的各组的频率为0.1、0.15、0.2、0.3、0.2、0.05,又知第二组的频数为18,则总篇数=第二组的频数÷第二组的频率;
(2)由图可以看出第四组的频率组大,则第四组的论文数量最多;
(3)第四组的论文的频数=120×0.3=36篇,第六组的论文的频数=120×0.05=6篇;则第四组的获奖率=20÷36=56%,第六组的获奖率为4÷6=67%;则第六组的获奖率较高.
点评:本题考查频率的意义,虽然题目没有直接告诉频率,但可以求出来;知道了频率、频数即及总数中的任何两个量就可以求第三个量.

练习册系列答案
相关题目
 组统计,绘制了频率分布直方图,已知从左至右各长方形的高的比为2:3:4:6:4:1,第二组的频数为18.请回答下列问题:
组统计,绘制了频率分布直方图,已知从左至右各长方形的高的比为2:3:4:6:4:1,第二组的频数为18.请回答下列问题: