Question

【题目】如图，在四边形ABCD中，AD=BC，∠B=∠D，AD不平行于BC，过点C作CE∥AD交△ABC的外接圆O于点E，连接AE．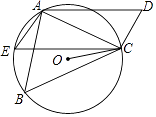
（1）求证：四边形AECD为平行四边形；
（2）连接CO，求证：CO平分∠BCE．

Answer 1

【答案】
（1）证明：由圆周角定理得，∠B=∠E，又∠B=∠D，

∴∠E=∠D，

∵CE∥AD，

∴∠D+∠ECD=180°，

∴∠E+∠ECD=180°，

∴AE∥CD，

∴四边形AECD为平行四边形；

（2）解：作OM⊥BC于M，ON⊥CE于N，

∵四边形AECD为平行四边形，

∴AD=CE，又AD=BC，

∴CE=CB，

∴OM=ON，又OM⊥BC，ON⊥CE，

∴CO平分∠BCE．

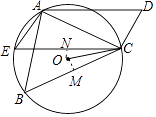
【解析】（1）根据圆周角定理得到∠B=∠E，得到∠E=∠D，根据平行线的判定和性质定理得到AE∥CD，证明结论；（2）作OM⊥BC于M，ON⊥CE于N，根据垂径定理、角平分线的判定定理证明．
【考点精析】认真审题，首先需要了解平行四边形的判定与性质(若一直线过平行四边形两对角线的交点，则这条直线被一组对边截下的线段以对角线的交点为中点，并且这两条直线二等分此平行四边形的面积)，还要掌握三角形的外接圆与外心(过三角形的三个顶点的圆叫做三角形的外接圆，其圆心叫做三角形的外心)的相关知识才是答题的关键．