题目内容
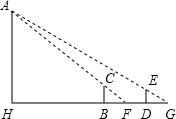
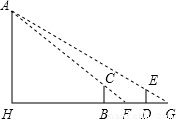
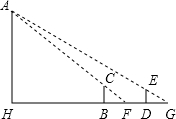如图，操场上有一根旗杆AH，为测量它的高度，在B和D处各立一根高1.5米的标杆BC、DE，两杆相距30米，测得视线AC与地面的交点为F，视线AE与地面的交点为G，并且H、B、F、D、G都在同一直线上，测得BF为3米，DG为5米，则旗杆AH的高度为分析：根据AH∥CB∥DE，可得△AHF∽△CBF，△AHG∽△EDG，可得
=
，
=
，即可求得AH的值，即可解题．
| BF |
| HF |
| CB |
| AH |
| DG |
| HG |
| DE |
| AH |
解答：解：由题意知，设AH=x，BH=y，
△AHF∽△CBF，△AHG∽△EDG，
∴
=
，
=
，
∴3x=1.5×（y+3）
5x=1.5×（y+30+5）
解得x=24，
故答案为 24．
△AHF∽△CBF，△AHG∽△EDG，
∴
| BF |
| HF |
| CB |
| AH |
| DG |
| HG |
| DE |
| AH |
∴3x=1.5×（y+3）
5x=1.5×（y+30+5）
解得x=24，
故答案为 24．
点评：本题考查了相似三角形对应边比值相等的性质，考查了平行线定理，本题中列出关于AH、BH的关系式并求解是解题的关键．
练习册系列答案
相关题目
30、某中学平整的操场上有一根旗杆（如图），一数学兴趣小组欲测量其高度，现有测量工具（皮尺、测角器、标杆）可供选用，请你用所学的知识，帮助他们设计测量方案．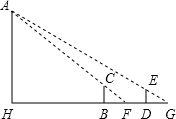
如图，操场上有一根旗杆AH，为测量它的高度，在B和D处各立一根高1.5米的标杆BC、DE，两杆相距30米，测得视线AC与地面的交点为F，视线AE与地面的交点为G，并且H、B、F、D、G都在同一直线上，测得BF为3米，DG为5米，则旗杆AH的高度为________米．
