题目内容
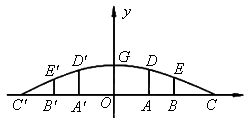
如图所示,这是某市一处十字路口立交桥的横断面在平面直角坐标系中的示意图,横断面的地平线为x轴,横断面的对称轴为y轴,拱桥的DG![]() 部分为一段抛物线,顶点G的高度为8米,AD和A
部分为一段抛物线,顶点G的高度为8米,AD和A![]() 是两侧高为5.5米的支柱,OA和
是两侧高为5.5米的支柱,OA和![]() 为两个方向的汽车通行区,宽都为15米,线段CD和C
为两个方向的汽车通行区,宽都为15米,线段CD和C![]() 为两段对称的上桥斜坡,其坡度为1∶4.
为两段对称的上桥斜坡,其坡度为1∶4.
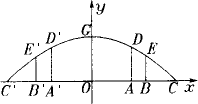
(1)求桥拱DG![]() 所在抛物线的解析式及C
所在抛物线的解析式及C![]() 的长;
的长;
(2)求BE和![]() 为支撑斜坡的立柱,其高都为4米,相应的AB和
为支撑斜坡的立柱,其高都为4米,相应的AB和![]() 为两个方向的行人及非机动车通行区,试求AB和
为两个方向的行人及非机动车通行区,试求AB和![]() 的宽.
的宽.
(3)按规定,汽车通行该桥下时载货最高处和桥拱之间的距离不得小于0.4米.今有一大型运货汽车,装载某大型设备后,其宽为4米,车载大型设备的顶部与地面的距离均为7米.它能否从OA(或![]() )区域安全通过?请说明理由.
)区域安全通过?请说明理由.
答案:
解析:
解析:
|
思路点拨:(1)由已知条件知抛物线的对称轴为y轴,可设抛物线解析式为y=ax2+k.由D、G两点坐标用待定系数法求出a、k的值.再用坡度求出C (2)由坡度求出AB和 (3)根据车子高度与纵坐标的大小,可作出判断. 评注:当抛物线的对称轴是y轴时,抛物线的解析式可设为y=ax2+c.然后根据已知条件用待定系数法求出a、c的值.货车通过抛物线型立交桥时,不但要考虑货车的宽度,更需要考虑其高度,本题还需要考虑货车顶部与抛物线弧之间还要留一定的间隙,考虑不周,实际问题中会产生撞车事故. |

练习册系列答案
相关题目

 24、美化城市,改善人们的居住环境已成为城市建设的一项重要内容.某市城区近几年来,通过拆迁旧房,植草,栽树,修建公园等措施,使城区绿地面积不断增加(如图所示)
24、美化城市,改善人们的居住环境已成为城市建设的一项重要内容.某市城区近几年来,通过拆迁旧房,植草,栽树,修建公园等措施,使城区绿地面积不断增加(如图所示)
 部分为一段抛物线,顶点G的高度为8米,AD和
部分为一段抛物线,顶点G的高度为8米,AD和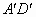 是两侧高为5.5米的支柱,OA和
是两侧高为5.5米的支柱,OA和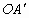 为两个方向的汽车通行区,宽都为15米,线段CD和
为两个方向的汽车通行区,宽都为15米,线段CD和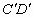 为两段对称的上桥斜坡,其坡度1:4.
为两段对称的上桥斜坡,其坡度1:4.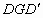 所在抛物线的关系式及
所在抛物线的关系式及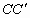 的长;
的长;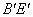 为支撑斜坡的立柱,其高都为4米,相应的AB和
为支撑斜坡的立柱,其高都为4米,相应的AB和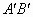 为两个方向的行人及非机动车通行区,试求AB和
为两个方向的行人及非机动车通行区,试求AB和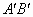 的宽;
的宽;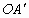 )区域安全通过?请说明理由.
)区域安全通过?请说明理由.