题目内容
| |||||||||||||||||||
解析：
(1) |
解：从图中可看出，骑自行车者先出发，他比骑摩托车者早出发3 h，而骑摩托车者先到达乙地，他比骑自行车者早到3 h. |
(2) |
观察正比例函数图象可知，骑自行车者从甲地到乙地共用了8 h，故其速度为 |
(3) |
由于骑自行车者在行驶过程中，其行驶路程与行驶时间足成正比例函数关系，且过点(8，80)，故其解析式可设为y＝kx，从而有80＝8 k，所以k＝10，即y＝10x；而骑摩托车者从甲地到乙地的行驶过程中，其行驶路程与行驶时间成一次函数关系，且过点(3，0)和点(5，80)，设其解析式为y＝kx＋b，则有 |
(4) |
从图象可以看出，他们在3～5 h(不包括3 h和5 h)都行驶在途中．故有： ①由题意可列不等式为10x＞40x－120，解得x＜4，即3＜x＜4时，自行车行驶在摩托车前面 ②由题意可列方程为10x＝40x－120，解得x＝4，即在自行车行驶了4 h时他们相遇 ③由题意可列不等式为10x＜40x－120，解得4＜x，故当4＜x＜5时，摩托车行驶在自行车前面． 解题指导：学会读图是中学生应具备的一项基本素质，通过逐步训练，要逐步掌握“架起”沟通图象语言与文字语言间的“桥梁”的方法，从而顺利实现两种语言的相互应用． |
＝10(km/h)；观察一次函数图象可知，骑摩托车者从甲地到乙地只用了2 h，故其速度为
＝40(km／h).
解得
故其解析式应为y＝40x－120
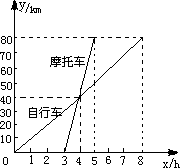
26、如图表示一骑自行车者和一骑摩托车者沿相同路线由甲地到乙地行驶过程的函数图象（分别为正比例函数和一次函数）．两地间的距离是80千米．请你根据图象回答或解决下面的问题：
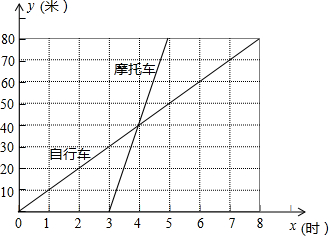两地间的距离是80千米．请你根据图象回答或解决下面的问题：
相同的路线由甲地到乙地行驶过程的函
数图象（分别是正比例函数图象和一次函数图象），两地间的距离是80千米，请你根据图象回答下列问题： 
早多长时间？谁到达乙地较早？早多长时间？