题目内容
已知抛物线![]() 与
与![]() 轴相交于点
轴相交于点![]() ,
,![]()
![]() ,且
,且![]() 是方程
是方程![]() 的两个实数根,点
的两个实数根,点![]() 为抛物线与
为抛物线与![]() 轴的交点.
轴的交点.
(1)求![]() 的值;
的值;
(2)分别求出直线![]() 和
和![]() 的解析式;
的解析式;
(3)若动直线![]() 与线段
与线段![]() 分别相交于
分别相交于![]() 两点,则在
两点,则在![]() 轴上是否存在点
轴上是否存在点![]() ,使得
,使得![]() 为等腰直角三角形(只求一种DE为腰或为底时)?若存在,求出点
为等腰直角三角形(只求一种DE为腰或为底时)?若存在,求出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
 |
解:(1)由![]() ,得
,得![]() .
. ![]() ,
,
把![]() 两点的坐标分别代入
两点的坐标分别代入![]() 联立求解,得
联立求解,得![]() .
.
(2)由(1)可得![]() ,
,![]() 当
当![]() 时,
时,![]() ,
,![]() .
.
设![]() ,把
,把![]() 两点坐标分别代入
两点坐标分别代入![]() ,联立求得
,联立求得
![]() .
.![]() 直线
直线![]() 的解析式为
的解析式为![]() .
.
同理可求得直线![]() 的解析式是
的解析式是![]() .
.
(3)假设存在满足条件的点![]() ,并设直线
,并设直线![]() 与
与![]() 轴的交点为
轴的交点为![]() .
.
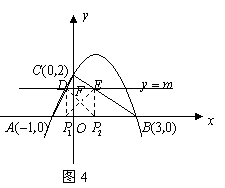 ①当
①当![]() 为腰时,分别过点
为腰时,分别过点![]() 作
作![]() 轴于
轴于![]() ,作
,作![]() 轴于
轴于![]() ,如图4,则
,如图4,则![]() 和
和![]() 都是等腰直角三角形,
都是等腰直角三角形,
![]() ,
,
![]() .
.
![]() ,
,![]() ,
,
![]() ,即
,即![]() .
.
解得![]() .
.
![]() 点
点![]() 的纵坐标是
的纵坐标是![]() ,
,![]() 点
点![]() 在直线
在直线![]() 上,
上,
![]() ,解得
,解得![]() ,
,![]() .
.
![]()
![]() ,同理可求
,同理可求![]() .
.
②当![]() 为底边时,
为底边时,
过![]() 的中点
的中点![]() 作
作![]() 轴于点
轴于点![]() ,如图5,
,如图5,
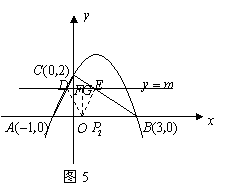 则
则![]() ,
,
由![]() ,
,
得![]() ,即
,即![]() ,
,
解得![]() .
.
同1方法.求得![]() ,
,
![]()
![]() ,
,![]() .
.
结合图形可知,![]() ,
,
![]() ,
,
![]() 是
是![]() ,
,![]() 也满足条件.
也满足条件.
综上所述,满足条件的点![]() 共有3个,即
共有3个,即![]() .
.

练习册系列答案
相关题目

 与
与 轴相交于A、B两点,其对称轴为直线
轴相交于A、B两点,其对称轴为直线 ,且与x轴交于点D,AO=1.
,且与x轴交于点D,AO=1. =_______。
=_______。 =_______,点B的坐标为(_______,_______):
=_______,点B的坐标为(_______,_______):
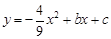 与
与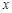 轴相交于A、B两点,其对称轴为直线
轴相交于A、B两点,其对称轴为直线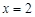 ,且与x轴交于点D,AO=1.
,且与x轴交于点D,AO=1.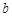 =_______。
=_______。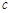 =_______,点B的坐标为(_______,_______):
=_______,点B的坐标为(_______,_______):
 与
与 轴相交于A、B两点,其对称轴为直线
轴相交于A、B两点,其对称轴为直线 ,且与x轴交于点D,AO=1.
,且与x轴交于点D,AO=1. =_______。
=_______。 =_______,点B的坐标为(_______,_______):
=_______,点B的坐标为(_______,_______):