题目内容
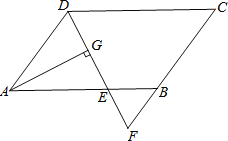
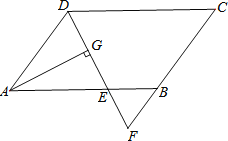
【题目】如图，在平行四边形ABCD中，AB=9，AD=6，∠ADC的平分线交AB于点E，交CB的延长线于点F，AG⊥DE，垂足为G．若AG=4
，则△BEF的面积是（ ）
A． B．2 C．3 D．4
【答案】B
【解析】
试题分析：首先利用已知条件可证明△ADE是等腰三角形，根据等腰三角形“三线合一”的性质得出DE=2DG，而在Rt△ADG中，由勾股定理可求得DG的值，即可求得DE的长；然后，证明△ADE∽△BFE，再分别求出△ADE的面积，然后根据面积比等于相似比的平方即可得到答案．
解：∵DE平分∠ADC，
∴∠ADE=∠CDE；
又∵四边形ABCD是平行四边形，
∴AB∥DC，
∴∠ADE=∠CDF=∠AED，
∴AD=AE=6，
∵AG⊥DE，垂足为G，
∴DE=2DG．
在Rt△ADG中，∵∠AGD=90°，AD=6，AG=4
，
∴DG=
=2，
∴DE=2DG=4；
∴S△ADE=
DEAG=×4×4
=8．
∵AE=6，AB=DC=9，
∴BE=AB﹣AE=9﹣6=3，
∴AE：BE=6：3=2：1．
∵AD∥FC，
∴△ADE∽△BFE，
∴S△ADE：S△BFE=（AE：BE）2=4：1，
则S△BEF=
S△ADE=2．
故选B．
练习册系列答案
相关题目
