题目内容
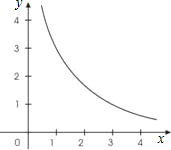 如图所示是反比例函数y=
如图所示是反比例函数y=| 2n-4 | x |
(1)图象的另一支在哪个象限?常数n的取值范围是什么?
(2)若函数图象经过点(3,1),求n的值;
(3)在这个函数图象的某一支上任取点A(a1,b1)和]点B(a2,b2),如果a1<a2,试比较b1和b2的大小.
分析:(1)根据反比例函数图象的性质,这一支位于第一象限,另一支一定位于第三象限;
(2)把点的坐标代入反比例函数求出n值,即可求出函数解析式;
(3)根据反比例函数图象的性质,当k>0时,在每个象限内,函数值y随x增大而减小解答.
(2)把点的坐标代入反比例函数求出n值,即可求出函数解析式;
(3)根据反比例函数图象的性质,当k>0时,在每个象限内,函数值y随x增大而减小解答.
解答:解:(1)图象的另一支在第三象限.(2分)
由图象可知,2n-4>0,解得:n>2(4分)
(2)将点(3,1)代入y=
得:1=
,
解得:n=
;(6分)
(3)∵2n-4>0,
∴在这个函数图象的任一支上,y随x增大而减小,
∴当a1<a2时,b1>b2.(8分)
由图象可知,2n-4>0,解得:n>2(4分)
(2)将点(3,1)代入y=
| 2n-4 |
| x |
| 2n-4 |
| 3 |
解得:n=
| 7 |
| 2 |
(3)∵2n-4>0,
∴在这个函数图象的任一支上,y随x增大而减小,
∴当a1<a2时,b1>b2.(8分)
点评:本题主要考查反比例函数图象的性质和待定系数法求函数解析式的方法,需要熟练掌握.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
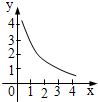 如图所示是反比例函数y=
如图所示是反比例函数y= 如图所示是反比例函数y=
如图所示是反比例函数y=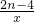 的图象的一支,据图象回答下列问题:
的图象的一支,据图象回答下列问题: 的图象的一支,根据图象回答下列问题:
的图象的一支,根据图象回答下列问题: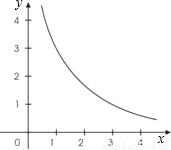
 的图象的一支,根据图象回答下列问题:
的图象的一支,根据图象回答下列问题: