题目内容
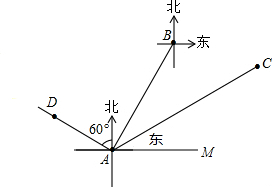 (2012•本溪二模)如图,在某海域内有三个港口A、C、D.港口C在港口A北偏东60°方向上,港口D在港口A北偏西60°方向上.一艘船以每小时25海里的速度沿北偏东30°的方向驶离A港口3小时后到达B点位置处,此时发现船舱漏水,同时在B处测得港口C在B处的南偏东75°方向上.若此船在B处向最近的港口停靠,应向A、C、D三个港口中的哪个港口停靠?并说明理由.
(2012•本溪二模)如图,在某海域内有三个港口A、C、D.港口C在港口A北偏东60°方向上,港口D在港口A北偏西60°方向上.一艘船以每小时25海里的速度沿北偏东30°的方向驶离A港口3小时后到达B点位置处,此时发现船舱漏水,同时在B处测得港口C在B处的南偏东75°方向上.若此船在B处向最近的港口停靠,应向A、C、D三个港口中的哪个港口停靠?并说明理由.分析:首先连接BC、BD,过B作BP⊥AC于点P.由已知得:∠BAD=90°,∠BAC=30°,∠ABC=105°,然后由三角函数的性质,可求得BC的长,继而求得答案.
解答: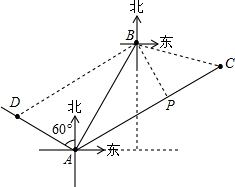 解:该船应向港口C停靠.
解:该船应向港口C停靠.
理由:连接BC、BD,过B作BP⊥AC于点P.
由已知得:∠BAD=90°,∠BAC=30°,∠ABC=105°,
∴∠C=45°,BD>AB,
在Rt△ABE中,AB=3×25=75(海里),
∴BP=
×75=
(海里).
在等腰Rt△CBP中,BC=
BP=
(海里),
∴BD>AB>BC.
∴该船应向港口C停靠.
 解:该船应向港口C停靠.
解:该船应向港口C停靠.理由:连接BC、BD,过B作BP⊥AC于点P.
由已知得:∠BAD=90°,∠BAC=30°,∠ABC=105°,
∴∠C=45°,BD>AB,
在Rt△ABE中,AB=3×25=75(海里),
∴BP=
| 1 |
| 2 |
| 75 |
| 2 |
在等腰Rt△CBP中,BC=
| 2 |
75
| ||
| 2 |
∴BD>AB>BC.
∴该船应向港口C停靠.
点评:此题考查了方向角问题.此题难度适中,注意构造直角三角形,并能借助于解直角三角形的知识求解是关键.

练习册系列答案
相关题目
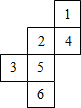 (2012•本溪二模)如图是正方体的展开图,则原正方体相对两个面上的数字之和的最小值是
(2012•本溪二模)如图是正方体的展开图,则原正方体相对两个面上的数字之和的最小值是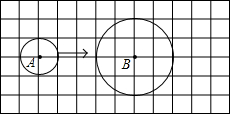 (2012•本溪二模)如图,在12×6的网格图中(每个小正方形的边长均为1个单位长),⊙A的半径为1,⊙B的半径为2,要使⊙A与静止的⊙B相切,那么⊙A由图示位置需向右平移
(2012•本溪二模)如图,在12×6的网格图中(每个小正方形的边长均为1个单位长),⊙A的半径为1,⊙B的半径为2,要使⊙A与静止的⊙B相切,那么⊙A由图示位置需向右平移