题目内容
下列求和的方法,相信你还未忘记:| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| n×(n-1) |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| n-1 |
| 1 |
| n |
请你据此知识解方程
| x |
| 1×2 |
| x |
| 2×3 |
| x |
| 3×4 |
| x |
| 2003×2004 |
我解得的结果是
分析:将原方程提出x化简得,x[(1-
)+(
-
)+(
-
)+…+(
-
)]=2003,再根据已知信息即可求得x的值.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 2003 |
| 1 |
| 2004 |
解答:解:∵
+
+
+…+
=(11-
)+(
-
)+(
-
)+…+(
-
)=…
∴
+
+
+…+
=2003可以化为:
x[(1-
)+(
-
)+(
-
)+…+(
-
)]=2003
x(1-
)=2003
x×
=2003
x=2004.
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| n×(n-1) |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| n-1 |
| 1 |
| n |
∴
| x |
| 1×2 |
| x |
| 2×3 |
| x |
| 3×4 |
| x |
| 2003×2004 |
x[(1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 2003 |
| 1 |
| 2004 |
x(1-
| 1 |
| 2004 |
x×
| 2003 |
| 2004 |
x=2004.
点评:本题是信息题,由信息中得出
=
-
,从而化简方程而求解.
| 1 |
| n×(n-1) |
| 1 |
| n-1 |
| 1 |
| n |

练习册系列答案
相关题目
 +
+ +
+ +…+
+…+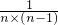 =(1-
=(1- )+(
)+( )+(
)+( )+…+(
)+…+( -
- )=…
)=…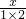 +
+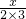 +
+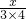 +…+
+…+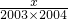 =2003
=2003 +
+ +
+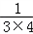 +…+
+…+ =(1﹣
=(1﹣ )+(
)+( ﹣
﹣ )+(
)+( ﹣
﹣ )+…+(
)+…+( ﹣
﹣ )=…,
)=…, +
+ +
+ +…+
+…+ =2003,
=2003,
 ,解得的结果是( )。
,解得的结果是( )。