题目内容
已知四个方程①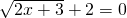 ;②
;②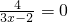 ;③
;③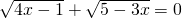 ;④
;④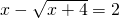 ,其中有实数解的方程的个数是 个.
,其中有实数解的方程的个数是 个.
- A.1
- B.2
- C.3
- D.4
A
分析:①根据被开方数为非负数即可判断;②根据分子不为0即可判断;③根据两个非负数相加为0,则两个数同时为0即可得出答案;④移项后两边平方即可求出x的值.
解答:方程①中得 ,无实数解,
,无实数解,
方程②中分子不为0,也没有实根,
方程③中若两个根式的和为0,则应同时满足4x-1=0和5-3x=0,相互矛盾,所以也没有实根,
只有方程④,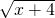 =x-2,两边同时平方,x+4=x2-4x+4,解得:x1=0(舍去),x2=5.
=x-2,两边同时平方,x+4=x2-4x+4,解得:x1=0(舍去),x2=5.
故选A.
点评:本题考查了无理方程,属于基础题,关键是掌握用平方法解无理方程.
分析:①根据被开方数为非负数即可判断;②根据分子不为0即可判断;③根据两个非负数相加为0,则两个数同时为0即可得出答案;④移项后两边平方即可求出x的值.
解答:方程①中得
 ,无实数解,
,无实数解,方程②中分子不为0,也没有实根,
方程③中若两个根式的和为0,则应同时满足4x-1=0和5-3x=0,相互矛盾,所以也没有实根,
只有方程④,
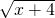 =x-2,两边同时平方,x+4=x2-4x+4,解得:x1=0(舍去),x2=5.
=x-2,两边同时平方,x+4=x2-4x+4,解得:x1=0(舍去),x2=5.故选A.
点评:本题考查了无理方程,属于基础题,关键是掌握用平方法解无理方程.

练习册系列答案
 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目