题目内容
按要求解下列两个方程:
(1)2x2+1=3x(配方法)
(2)3x2+6x-4=0(公式法)
解:(1)移项得:2x2-3x=-1,
系数化为1得:x2- x=-
x=- ,
,
配方得:x2- x+
x+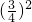 =-
=- +
+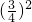 ,
,
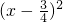 =
= ,
,
开方得:x- =
= ,x-
,x- =-
=- ,
,
解得:x1=1,x2= .
.
(2)∵a=3,b=6,c=-4,
∴b2-4ac=62-4×3×(-4)=84,
∴x= =
= ,
,
即x1= ,x2=-
,x2=- .
.
分析:(1)移项后方程两边都除以2得出x2- x=-
x=- ,配方得出
,配方得出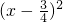 =
= ,开方得出方程x-
,开方得出方程x- =
= ,x-
,x- =-
=- ,求出方程的解即可;
,求出方程的解即可;
(2)求出b2-4ac的值,代入公式x=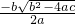 求出即可.
求出即可.
点评:本题考查了解一元二次方程的应用,解(1)小题的关键是配方,解(2)小题的关键是能熟练地运用公式进行计算,题目都比较好,难度适中.
系数化为1得:x2-
 x=-
x=- ,
,配方得:x2-
 x+
x+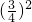 =-
=- +
+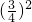 ,
,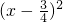 =
= ,
,开方得:x-
 =
= ,x-
,x- =-
=- ,
,解得:x1=1,x2=
 .
.(2)∵a=3,b=6,c=-4,
∴b2-4ac=62-4×3×(-4)=84,
∴x=
 =
= ,
,即x1=
 ,x2=-
,x2=- .
.分析:(1)移项后方程两边都除以2得出x2-
 x=-
x=- ,配方得出
,配方得出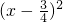 =
= ,开方得出方程x-
,开方得出方程x- =
= ,x-
,x- =-
=- ,求出方程的解即可;
,求出方程的解即可;(2)求出b2-4ac的值,代入公式x=
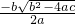 求出即可.
求出即可.点评:本题考查了解一元二次方程的应用,解(1)小题的关键是配方,解(2)小题的关键是能熟练地运用公式进行计算,题目都比较好,难度适中.

练习册系列答案
相关题目
 (配方法) (2)
(配方法) (2) (公式法)
(公式法)