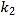Question

【题目】如图，在数轴上点A表示的数为a，点B表示的数为b，且a，b满足|a+2|+（3a+b）2=0，O为原点．

（1）则a= ，b= ；

（2）若动点P从点A出发，以每秒1个单位长度的速度沿数轴向右匀速运动，

①当PO=2PB时，求点P的运动时间t；

②当点P运动到线段OB上时，分别取AP和OB的中点E、F，则的值是否为一个定值？如果是，求出定值，如果不是，说明理由.

Answer 1

【答案】（1）-2，6；（2）①点P的运动时间t为6或14秒；②的值是一个定值， =2.

【解析】试题分析：（1）根据非负数的性质即可求出a、b的值；

（2）①先表示出运动t秒后P点对应的数为－2＋t，再根据两点间的距离公式得出PO＝|－2＋t|，PB＝|－2＋t－6|＝|t－8|，利用PO＝2PB建立方程，求解即可；

②根据中点坐标公式分别表示出点E表示的数，点F表示的数，再计算即可；

试题解析：

（1）∵|a＋2|＋（3a＋b）2＝0，

∴a＋2＝0，3a＋b＝0，

∴a＝－2，b＝6，

故答案为：－2，6；

（2）①∵若动点P从点A出发，以每秒1个单位长度的速度沿数轴向右匀速运动，

∴运动t秒后P点对应的数为－2＋t，

∵点A表示的数为－2，点B表示的数为6，

∴PO＝|－2＋t|，PB＝|－2＋t－6|＝|t－8|，

当PO＝2PB时，有|－2＋t|＝2|t－8|，

解得t＝6或14，

答：点P的运动时间t为6或14秒；

②的值是一个定值，

当点P运动到线段OB上时，

AP中点E表示的数是 ，OB的中点F表示的数是3，

所以EF＝3－ ＝，

则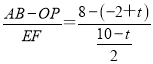 ＝2.