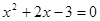题目内容
下列一元二次方程中两根之和为2的是
- A.x2-2x+3=0
- B.x2+2x+3=0
- C.x2-2x-3=0
- D.x2+2x-3=0
C
分析:先根据根的判别式,判断有无实数根的情况,再根据根与系数的关系,利用x1+x2=- 计算即可.
计算即可.
解答:A、∵x2-2x+3=0,
∴△=b2-4ac=-8<0,
∴此方程没有实数根,
故此选项错误;
B、∵x2+2x+3=0,
∴△=b2-4ac=-8<0,
∴此方程没有实数根,
故此选项错误;
C、∵x2-2x-3=0,
∴△=b2-4ac=16>0,
∴此方程有实数根,
根据根与系数的关系可求x1+x2=- =-
=-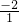 =2,
=2,
故此选项正确;
D、∵x2+2x-3=0,
∴△=b2-4ac=16>0,
∴此方程有实数根,
根据根与系数的关系可求x1+x2=- =-
=-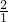 =-2,
=-2,
故此选项错误.
故选C.
点评:本题综合考查了根的判别式和根与系数的关系.利用根的判别式判断时,注意若△<0,则方程没有实数根;若△≥0,则方程有实数根.
分析:先根据根的判别式,判断有无实数根的情况,再根据根与系数的关系,利用x1+x2=-
 计算即可.
计算即可.解答:A、∵x2-2x+3=0,
∴△=b2-4ac=-8<0,
∴此方程没有实数根,
故此选项错误;
B、∵x2+2x+3=0,
∴△=b2-4ac=-8<0,
∴此方程没有实数根,
故此选项错误;
C、∵x2-2x-3=0,
∴△=b2-4ac=16>0,
∴此方程有实数根,
根据根与系数的关系可求x1+x2=-
 =-
=-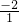 =2,
=2,故此选项正确;
D、∵x2+2x-3=0,
∴△=b2-4ac=16>0,
∴此方程有实数根,
根据根与系数的关系可求x1+x2=-
 =-
=-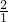 =-2,
=-2,故此选项错误.
故选C.
点评:本题综合考查了根的判别式和根与系数的关系.利用根的判别式判断时,注意若△<0,则方程没有实数根;若△≥0,则方程有实数根.

练习册系列答案
相关题目
下列一元二次方程中两根之和为2的是( )
| A、x2-2x+3=0 | B、x2+2x+3=0 | C、x2-2x-3=0 | D、x2+2x-3=0 |
下列一元二次方程中两实数根之和为2的是 ( )
A.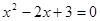 ; ; | B. ; ; |
C.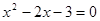 ; ; | D. . . |
 ; B.
; B.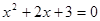 ;
; ; D.
; D. .
.
 B.
B.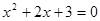 C.
C.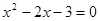 D.
D.