题目内容
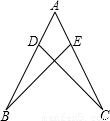
(2006•肇庆)如图,在△ABC中,AB=AC,点D,E分别是AB,AC的中点,F是BC延长线上的一点,且CF= BC.
BC.(1)求证:DE=CF;(2)求证:BE=EF.

【答案】分析:(1)根据三角形的中位线定理证明DE= BC,再结合已知条件证明结论;
BC,再结合已知条件证明结论;
(2)在(1)的结论的基础上,连接CD,发现平行四边形DEFC和等腰梯形DECB.
根据平行四边形的性质得到CD=EF;根据等腰梯形的性质得到CD=BE.从而得到BE=EF.
解答: 证明:(1)∵D,E分别为AB,AC的中点,
证明:(1)∵D,E分别为AB,AC的中点,
∴DE为中位线.
∴DE∥BC,且DE= BC.
BC.
又∵CF= BC,
BC,
∴DE=CF.
(2)连接DC,
由(1)可得DE∥CF,且DE=CF,
∴四边形DCFE为平行四边形.
∴EF=DC.
∵AB=AC,且DE为中位线,
∴四边形DBCE为等腰梯形.
又∵DC,BE为等腰梯形DBCE的对角线,
∴DC=BE.
∴BE=EF.
点评:此题主要是根据三角形的中位线定理发现平行四边形和等腰梯形,再根据平行四边形的性质和等腰梯形的性质进行证明.
 BC,再结合已知条件证明结论;
BC,再结合已知条件证明结论;(2)在(1)的结论的基础上,连接CD,发现平行四边形DEFC和等腰梯形DECB.
根据平行四边形的性质得到CD=EF;根据等腰梯形的性质得到CD=BE.从而得到BE=EF.
解答:
 证明:(1)∵D,E分别为AB,AC的中点,
证明:(1)∵D,E分别为AB,AC的中点,∴DE为中位线.
∴DE∥BC,且DE=
 BC.
BC.又∵CF=
 BC,
BC,∴DE=CF.
(2)连接DC,
由(1)可得DE∥CF,且DE=CF,
∴四边形DCFE为平行四边形.
∴EF=DC.
∵AB=AC,且DE为中位线,
∴四边形DBCE为等腰梯形.
又∵DC,BE为等腰梯形DBCE的对角线,
∴DC=BE.
∴BE=EF.
点评:此题主要是根据三角形的中位线定理发现平行四边形和等腰梯形,再根据平行四边形的性质和等腰梯形的性质进行证明.

练习册系列答案
相关题目



 ?
?