题目内容
等腰△ABC,AB=AC=8,∠BAC=120°,P为BC的中点,小慧拿着含30°角的透明三角板,使30°角的顶点落在点P,三角板绕P点旋转.
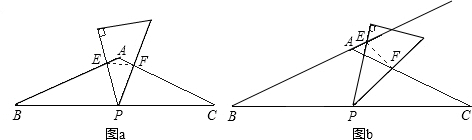
(1)如图a,当三角板的两边分别交AB、AC于点E、F时.求证:△BPE∽△CFP;
(2)操作:将三角板绕点P旋转到图b情形时,三角板的两边分别交BA的延长线、边AC于点E、F.
①探究1:△BPE与△CFP还相似吗?(只需写出结论)
②探究2:连接EF,△BPE与△PFE是否相似?请说明理由;
③设EF=m,△EPF的面积为S,试用m的代数式表示S.
(1)证明:∵在△ABC中,∠BAC=120°,AB=AC,
∴∠B=∠C=30°.
∵∠B+∠BPE+∠BEP=180°,
∴∠BPE+∠BEP=150°,
又∠EPF=30°,且∠BPE+∠EPF+∠CPF=180°,
∴∠BPE+∠CPF=150°,
∴∠BEP=∠CPF,
∴△BPE∽△CFP(两角对应相等的两个三角形相似).
(2)解:①△BPE∽△CFP;
②△BPE与△PFE相似.
下面证明结论:
同(1),可证△BPE∽△CFP,得 =
= ,而CP=BP,因此
,而CP=BP,因此 .
.
又因为∠EBP=∠EPF,所以△BPE∽△PFE(两边对应成比例且夹角相等的两个三角形相似).
③由②得△BPE∽△PFE,所以∠BEP=∠PEF.
分别过点P作PM⊥BE,PN⊥EF,垂足分别为M、N,则PM=PN.
连AP,在Rt△ABP中,由∠B=30°,AB=8,可得AP=4.
所以PM=2 ,所以PN=2
,所以PN=2 ,
,
所以s= PN×EF=
PN×EF= m.
m.
分析:(1)找出△BPE与△CFP的对应角,其中∠BPE+∠CPF=150°,∠CPF+∠CFP=150°,得出∠BPE=∠CFP,从而解决问题;
(2)①小题同前可证,②小题可通过对应边成比例证明,③小题求出△BPE中BE上的高,求出△PEF中EF上的高,得出关系式.
点评:这是一道操作探究题,它改变了多年来扬州市最后一道压轴题以二次函数为主线的呈现方式.它以每位学生都有的30°三角板在图形上的运动为背景,既考查了学生图形旋转变换的思想,静中思动,动中求静的思维方法,又考查了学生动手实践、自主探究的能力.
问题的设置以问题串的形式呈现,层层推进,第1问入手容易,第2问深入困难,有一定的区分度,使不同层次的学生有不同的收获.
同时通过本题的解答,一使同学们领悟到学习数学的方法,二是提醒教师学生在平时的教学中要注意变式练习.
本题的第1问不难,用两角相等即可证得相似,第2问中的①由第1问类比即得,②要用到①中对应边成比例代换后方可证得,③一般学生都能想到作高,却想不到求这条高要用到角平分线、解直角三角形等知识.
实际上三角板运动到特殊位置还有一些结论,感兴趣的学生不妨继续研究.
要关注几何图形在运动状态下几何关系的不变性哦!
∴∠B=∠C=30°.
∵∠B+∠BPE+∠BEP=180°,
∴∠BPE+∠BEP=150°,
又∠EPF=30°,且∠BPE+∠EPF+∠CPF=180°,
∴∠BPE+∠CPF=150°,
∴∠BEP=∠CPF,
∴△BPE∽△CFP(两角对应相等的两个三角形相似).
(2)解:①△BPE∽△CFP;
②△BPE与△PFE相似.
下面证明结论:
同(1),可证△BPE∽△CFP,得
 =
= ,而CP=BP,因此
,而CP=BP,因此 .
.又因为∠EBP=∠EPF,所以△BPE∽△PFE(两边对应成比例且夹角相等的两个三角形相似).
③由②得△BPE∽△PFE,所以∠BEP=∠PEF.

分别过点P作PM⊥BE,PN⊥EF,垂足分别为M、N,则PM=PN.
连AP,在Rt△ABP中,由∠B=30°,AB=8,可得AP=4.
所以PM=2
 ,所以PN=2
,所以PN=2 ,
,所以s=
 PN×EF=
PN×EF= m.
m.分析:(1)找出△BPE与△CFP的对应角,其中∠BPE+∠CPF=150°,∠CPF+∠CFP=150°,得出∠BPE=∠CFP,从而解决问题;
(2)①小题同前可证,②小题可通过对应边成比例证明,③小题求出△BPE中BE上的高,求出△PEF中EF上的高,得出关系式.
点评:这是一道操作探究题,它改变了多年来扬州市最后一道压轴题以二次函数为主线的呈现方式.它以每位学生都有的30°三角板在图形上的运动为背景,既考查了学生图形旋转变换的思想,静中思动,动中求静的思维方法,又考查了学生动手实践、自主探究的能力.
问题的设置以问题串的形式呈现,层层推进,第1问入手容易,第2问深入困难,有一定的区分度,使不同层次的学生有不同的收获.
同时通过本题的解答,一使同学们领悟到学习数学的方法,二是提醒教师学生在平时的教学中要注意变式练习.
本题的第1问不难,用两角相等即可证得相似,第2问中的①由第1问类比即得,②要用到①中对应边成比例代换后方可证得,③一般学生都能想到作高,却想不到求这条高要用到角平分线、解直角三角形等知识.
实际上三角板运动到特殊位置还有一些结论,感兴趣的学生不妨继续研究.
要关注几何图形在运动状态下几何关系的不变性哦!

练习册系列答案
相关题目
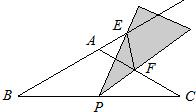 等腰△ABC,AB=AC,∠BAC=120°,P为BC上的中点,小慧拿着含30°角的透明三角板,使30°角的顶点落在点P处,三角板绕点P旋转到如图所示情形时,三角板的两边分别交BA的延长线于点E,交边AC于点F,连接EF,△BPE与△PFE是否相似?请说明理由.
等腰△ABC,AB=AC,∠BAC=120°,P为BC上的中点,小慧拿着含30°角的透明三角板,使30°角的顶点落在点P处,三角板绕点P旋转到如图所示情形时,三角板的两边分别交BA的延长线于点E,交边AC于点F,连接EF,△BPE与△PFE是否相似?请说明理由.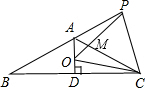 如图,在等腰△ABC中AB=AC,∠BAC=120°,AD⊥BC于点D,点P是BA延长线上一点,点O是线段AD上一点,OP=OC,OP与AC相交与点M,则下列结论:
如图,在等腰△ABC中AB=AC,∠BAC=120°,AD⊥BC于点D,点P是BA延长线上一点,点O是线段AD上一点,OP=OC,OP与AC相交与点M,则下列结论: 已知等腰△ABC,AB=AC=4,∠BAC=120°,请用圆规和直尺作出△ABC的外接圆.并计算此外接圆的半径.
已知等腰△ABC,AB=AC=4,∠BAC=120°,请用圆规和直尺作出△ABC的外接圆.并计算此外接圆的半径.