题目内容
一个半径为1cm的圆,在边长为6cm的正六边形内任意挪动(圆可以与正六边形的边相切),则圆在正六边形内不能达到的部分的面积为分析:小圆不能达到的是每个顶点出的六小块,每小块的面积等于四边形的面积,即两个全等的直角三角形的面积的和,减去圆的面积的
,据此即可求解.
| 1 |
| 6 |
解答: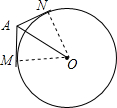 解:如图,小圆不能达到的是每个顶点出的六小块,
解:如图,小圆不能达到的是每个顶点出的六小块,
每小块的面积是2 S△OAM-
S圆O=
×1-
π=
-
.
故六小块的面积的和是2
-π.
故答案是:2
-π.
 解:如图,小圆不能达到的是每个顶点出的六小块,
解:如图,小圆不能达到的是每个顶点出的六小块,每小块的面积是2 S△OAM-
| 1 |
| 6 |
| ||
| 3 |
| 1 |
| 6 |
| ||
| 3 |
| π |
| 6 |
故六小块的面积的和是2
| 3 |
故答案是:2
| 3 |
点评:本题主要考查了正多边形的计算,正确理解小圆不能到达的部分是每个顶点出的六小块,是解决本题的关键.

练习册系列答案
相关题目