Question

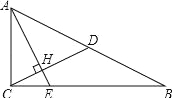
【题目】如图，已知Rt△ABC中，∠ACB=90°，CD是斜边AB上的中线，过点A作AE⊥CD，AE分别与CD、CB相交于点H、E，AH=2CH．

（1）求sinB的值；

（2）如果CD=，求BE的值．

Answer 1

【答案】(1)；(2) 3．

【解析】

试题分析：（1）根据∠ACB=90°，CD是斜边AB上的中线，可得出CD=BD，则∠B=∠BCD，再由AE⊥CD，可证明∠B=∠CAH，由AH=2CH，可得出CH：AC=1：，即可得出sinB的值；

（2）根据sinB的值，可得出AC：AB=1：，再由AB=，得AC=2，则CE=1，从而得出BE．

试题解析：（1）∵∠ACB=90°，CD是斜边AB上的中线，

∴CD=BD，

∴∠B=∠BCD，

∵AE⊥CD，

∴∠CAH+∠ACH=90°，

又∠ACB=90°，

∴∠BCD+∠ACH=90°，

∴∠B=∠BCD=∠CAH，即∠B=∠CAH，

∵AH=2CH，

∴由勾股定理得AC=CH，

∴CH：AC=1：，

∴sinB=；

（2）∵sinB=，

∴AC：AB=1：，

∴AC=2．

∵∠CAH=∠B，

∴sin∠CAH=sinB==，

设CE=x（x＞0），则AE=x，则，

∴CE=x=1，AC=2，

在Rt△ABC中，，

∵AB=2CD=，

∴BC=4，

∴BE=BC﹣CE=3．