题目内容
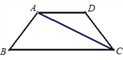
【题目】已知：如图，AD∥BC，AB=CD，对角线CA平分∠BCD，AD=5，tanB=
，求BC的长．
【答案】13
【解析】分析：作梯形的两条高，构造了一个矩形和两个直角三角形．根据角平分线的定义和平行线的性质得到等腰
，即
再根据锐角三角函数的概念得到
结合勾股定理得到从而求得BE的长，再进一步计算出
和
的长．
详解：过点A作AE⊥BC，垂足为E，过点D作DF⊥BC，垂足为F，如下图所示，
∵AC平分∠BCD，
∴∠1=∠2.
∵AD∥BC，
∴∠2=∠3.
∴∠1=∠3.
∴AD=DC.∵AD=5，AB=DC，
∴AD=DC=AB=5.
过点A作AE⊥BC于点E，过点D作DF⊥BC于点F.
∴
在Rt△AEB中，
设AE=3x，则BE=4x.
∵AB=5，
∴
∴x=1(负值舍去).
∴AE=3，BE=4.同理可得FC=4.
∵AE⊥BC，DF⊥BC，
∴AE∥DF.
∵AD∥BC，
∴四边形AEFD是平行四边形。
∴EF=AD=5.
∴BC=13.
练习册系列答案
相关题目
