Question

如图，直线y＝－x＋3与x轴、y轴分别相交于点B、点C，经过B、C两点的抛物线y＝ax²＋bx＋c与x轴的另一个交点为A，顶点为P，且对称轴是直线x＝2．

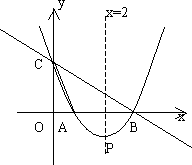
(1)求该抛物线的函数表达式；

(2)若点R在(1)中抛物线的对称轴上，且使得△RAC的周长最小，求点R的坐标；

(3)该Q为(1)中抛物线对称轴上一点，在抛物线上是否存在这样一点M，使得以A、B、Q、M为顶点的四边形是平行四边形．若存在，求出点M的坐标；若不存在，请说明理由．

Answer 1

答案：
解析：

(1)由已知得：，， 　　∵对称轴是　∴ 　　∴设 　　把点C代入得： 　　∴　　(4分) 　　(2)∵点A与点B关于直线对称，则直线BC与对称轴的交点就是所求的点R，∴当时， 　　∴　　(4分) 　　(3) 　　∴ 　　①当为时， 　　②∵AB＝2，当时，　∴ 　　③当时，，∴ 　　∴的坐标是，，　　(6分)