题目内容
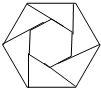 如图,把正六边形各边按同一方向延长,使延长的线段与原正六边形的边长相等,顺次连接这六条线段外端点可以得到一个新的正六边形,重复上述过程,经过10次后,所得到的正六边形是原正六边形边长的
如图,把正六边形各边按同一方向延长,使延长的线段与原正六边形的边长相等,顺次连接这六条线段外端点可以得到一个新的正六边形,重复上述过程,经过10次后,所得到的正六边形是原正六边形边长的分析:先根据正六边形的性质得出∠1的度数,再根据AD=CD=BC判断出△ABC的形状及∠2的度数,求出AB的长,进而可得出,经过10次后,所得到的正六边形是原正六边形边长的倍数.
解答: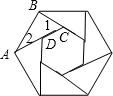

解:∵此六边形是正六边形,
∴∠1=180°-120°=60°,
∵AD=CD=BC,
∴△BCD为等边三角形,
∴BD=
AC,
∴△ABC是直角三角形
又BC=
AC,
∴∠2=30°,
∴AB=
BC=
CD,
同理可得,经过2次后,所得到的正六边形是原正六边形边长(
)2=3倍,
∴经过10次后,所得到的正六边形是原正六边形边长的(
)10=243倍.
故答案为:243.


解:∵此六边形是正六边形,
∴∠1=180°-120°=60°,
∵AD=CD=BC,
∴△BCD为等边三角形,
∴BD=
| 1 |
| 2 |
∴△ABC是直角三角形
又BC=
| 1 |
| 2 |
∴∠2=30°,
∴AB=
| 3 |
| 3 |
同理可得,经过2次后,所得到的正六边形是原正六边形边长(
| 3 |
∴经过10次后,所得到的正六边形是原正六边形边长的(
| 3 |
故答案为:243.
点评:本题考查的是正多边形和圆,解答此题的关键是熟知正多边形内角的性质及直角三角形的判定定理.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
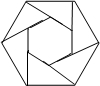 (2013•玉田县一模)如图,把正六边形各边按同一方向延长,使延长的线段长度与原正六边形的长度相等,顺次连接这六条线段外端点可以得到一个新的正六边形,重复上述过程,经过8次后,所得到的正六边形的边长是原六边形边长的
(2013•玉田县一模)如图,把正六边形各边按同一方向延长,使延长的线段长度与原正六边形的长度相等,顺次连接这六条线段外端点可以得到一个新的正六边形,重复上述过程,经过8次后,所得到的正六边形的边长是原六边形边长的

