题目内容
【题目】已知:如图,在△ABC中,AB=AC,以AC为直径的⊙O交AB于点M,交BC于点N,连接AN,过点C的切线交AB的延长线于点P.
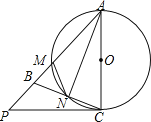
(1)求证:∠BCP=∠BAN
(2)求证:![]() =
=![]() .
.
【答案】见解析
【解析】
试题分析:(1)由AC为⊙O直径,得到∠NAC+∠ACN=90°,由AB=AC,得到∠BAN=∠CAN,根据PC是⊙O的切线,得到∠ACN+∠PCB=90°,于是得到结论.
(2)由等腰三角形的性质得到∠ABC=∠ACB,根据圆内接四边形的性质得到∠PBC=∠AMN,证出△BPC∽△MNA,即可得到结论.
(1)证明:∵AC为⊙O直径,
∴∠ANC=90°,
∴∠NAC+∠ACN=90°,
∵AB=AC,
∴∠BAN=∠CAN,
∵PC是⊙O的切线,
∴∠ACP=90°,
∴∠ACN+∠PCB=90°,
∴∠BCP=∠CAN,
∴∠BCP=∠BAN;
(2)∵AB=AC,
∴∠ABC=∠ACB,
∵∠PBC+∠ABC=∠AMN+∠ACN=180°,
∴∠PBC=∠AMN,
由(1)知∠BCP=∠BAN,
∴△BPC∽△MNA,
∴![]() .
.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目