题目内容
【题目】如图1,已知线段AB、CD相交于点O,连接AC、BD,我们把形如图1的图形称之为“8字形”.如图2,∠CAB和∠BDC的平分线AP和DP相交于点P,并且与CD、AB分别相交于M、N.试解答下列问题:
(1)仔细观察,在图2中有 个以线段AC为边的“8字形”;
(2)在图2中,若∠B=96°,∠C=100°,求∠P的度数.
(3)在图2中,若设∠C=α,∠B=β,∠CAP=![]() ∠CAB,∠CDP=
∠CAB,∠CDP=![]() ∠CDB,试问∠P与∠D、∠B之间存在着怎样的数量关系(用α、β表示∠P),并说明理由;
∠CDB,试问∠P与∠D、∠B之间存在着怎样的数量关系(用α、β表示∠P),并说明理由;
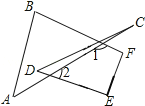
(4)如图3,则∠A+∠B+∠C+∠D+∠E+∠F的度数为 .

【答案】360°
【解析】
试题分析:(1)以M为交点的“8字形”有1个,以O为交点的“8字形”有2个;
(2)根据角平分线的定义得到∠CAP=∠BAP,∠BDP=∠CDP,再根据三角形内角和定理得到∠CAP+∠C=∠CDP+∠P,∠BAP+∠P=∠BDP+∠B,两等式相减得到∠C﹣∠P=∠P﹣∠B,即∠P=![]() (∠C+∠B),然后把∠C=100°,∠B=96°代入计算即可;
(∠C+∠B),然后把∠C=100°,∠B=96°代入计算即可;
(3)与(2)的证明方法一样得到∠P=![]() (2∠C+∠B).
(2∠C+∠B).
(4)根据三角形内角与外角的关系可得∠B+∠A=∠1,∠C+∠D=∠2,再根据四边形内角和为360°可得答案.
解:(1)在图2中有3个以线段AC为边的“8字形”,
故答案为3;
(2)∵∠CAB和∠BDC的平分线AP和DP相交于点P,
∴∠CAP=∠BAP,∠BDP=∠CDP,
∵∠CAP+∠C=∠CDP+∠P,∠BAP+∠P=∠BDP+∠B,
∴∠C﹣∠P=∠P﹣∠B,
即∠P=![]() (∠C+∠B),
(∠C+∠B),
∵∠C=100°,∠B=96°
∴∠P=![]() (100°+96°)=98°;
(100°+96°)=98°;
(3)∠P=![]() (β+2α);
(β+2α);
理由:∵∠CAP=![]() ∠CAB,∠CDP=
∠CAB,∠CDP=![]() ∠CDB,
∠CDB,
∴∠BAP=![]() ∠BAC,∠BDP=
∠BAC,∠BDP=![]() ∠BDC,
∠BDC,
∵∠CAP+∠C=∠CDP+∠P,∠BAP+∠P=∠BDP+∠B,
∴∠C﹣∠P=![]() ∠BDC﹣
∠BDC﹣![]() ∠BAC,∠P﹣∠B=
∠BAC,∠P﹣∠B=![]() ∠BDC﹣
∠BDC﹣![]() ∠BAC,
∠BAC,
∴2(∠C﹣∠P)=∠P﹣∠B,
∴∠P=![]() (∠B+2∠C),
(∠B+2∠C),
∵∠C=α,∠B=β,
∴∠P=![]() (β+2α);
(β+2α);
(4)∵∠B+∠A=∠1,∠C+∠D=∠2,
∴∠A+∠B+∠C+∠D=∠1+∠2,
∵∠1+∠2+∠F+∠E=360°,
∴∠A+∠B+∠C+∠D+∠E+∠F=360°.
故答案为:360°.