Question

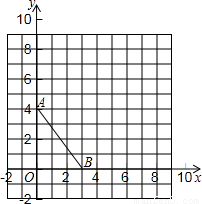
△OAB的坐标分别为O（0，0），A（0，4），B（3，0），以原点为位似中心，在第一象限将△OAB扩大，使变换得到的△OEF与△OAB对应边的比为2：1，
（1）画出△OEF；
（2）求四边形ABFE的面积．

Answer 1

解：（1）作出相应的图形，如图所示；
（2）由题意得：OA=4，OB=3，OE=8，OF=6，△OAB与△EOF都为直角三角形，
则S_{四边形ABFE}=S_△OEF-S_△OAB
=OF•OE-OB•OA
=×6×8-×3×4
=24-6
=18．
分析：（1）根据题意作出相应的图形，如图所示；
（2）由图形求出OA，OB，OE，OF的长，四边形ABFE的面积=三角形EOF面积-三角形AOB面积，求出即可．
点评：此题考查了作图-位似变换，画位似图形的一般步骤为：①确定位似中心，②分别连接并延长位似中心和能代表原图的关键点；③根据相似比，确定能代表所作的位似图形的关键点；顺次连接上述各点，得到放大或缩小的图形．