题目内容
如图,P是定长线段AB上一点,C、D两点分别从P、B出发以1cm/s、2cm/s的速度沿直线AB向左运动(C在线段AP上,D在线段BP上)
(1)若C、D运动到任一时刻时,总有PD=2AC,请说明P点在线段AB上的位置:

(2)在(1)的条件下,Q是直线AB上一点,且AQ-BQ=PQ,求
的值.

(3)在(1)的条件下,若C、D运动5秒后,恰好有CD=
AB,此时C点停止运动,D点继续运动(D点在线段PB上),M、N分别是CD、PD的中点,下列结论:①PM-PN的值不变;②
的值不变,可以说明,只有一个结论是正确的,请你找出正确的结论并求值.

(1)若C、D运动到任一时刻时,总有PD=2AC,请说明P点在线段AB上的位置:

(2)在(1)的条件下,Q是直线AB上一点,且AQ-BQ=PQ,求
| PQ |
| AB |

(3)在(1)的条件下,若C、D运动5秒后,恰好有CD=
| 1 |
| 2 |
| MN |
| AB |

(1)根据C、D的运动速度知:BD=2PC
∵PD=2AC,
∴BD+PD=2(PC+AC),即PB=2AP,
∴点P在线段AB上的
处;
(2)如图:

∵AQ-BQ=PQ,
∴AQ=PQ+BQ;
又AQ=AP+PQ,
∴AP=BQ,
∴PQ=
AB,
∴
=
.
当点Q'在AB的延长线上时
AQ'-AP=PQ'
所以AQ'-BQ'=PQ=AB
所以
=1;
(3)②
的值不变.
理由:如图,当点C停止运动时,有CD=
AB,
∴CM=
AB;
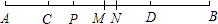
∴PM=CM-CP=
AB-5,
∵PD=PB-BD=
AB-10,
∴PN=
(
AB-10)=
AB-5,
∴MN=PN-PM=
AB;
当点C停止运动,D点继续运动时,MN的值不变,所以,
=
=
.
∵PD=2AC,
∴BD+PD=2(PC+AC),即PB=2AP,
∴点P在线段AB上的
| 1 |
| 3 |
(2)如图:

∵AQ-BQ=PQ,
∴AQ=PQ+BQ;
又AQ=AP+PQ,
∴AP=BQ,
∴PQ=
| 1 |
| 3 |
∴
| PQ |
| AB |
| 1 |
| 3 |
当点Q'在AB的延长线上时
AQ'-AP=PQ'
所以AQ'-BQ'=PQ=AB
所以
| PQ |
| AB |
(3)②
| MN |
| AB |
理由:如图,当点C停止运动时,有CD=
| 1 |
| 2 |
∴CM=
| 1 |
| 4 |
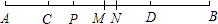
∴PM=CM-CP=
| 1 |
| 4 |
∵PD=PB-BD=
| 2 |
| 3 |
∴PN=
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| 3 |
∴MN=PN-PM=
| 1 |
| 12 |
当点C停止运动,D点继续运动时,MN的值不变,所以,
| MN |
| AB |
| ||
| AB |
| 1 |
| 12 |

练习册系列答案
相关题目



