题目内容
 如图,已知两圆内切于A,过外圆直径AB的一端B引外圆的弦BD与内圆切于C点,若BC=m,CD=n,求两圆半径的长.
如图,已知两圆内切于A,过外圆直径AB的一端B引外圆的弦BD与内圆切于C点,若BC=m,CD=n,求两圆半径的长.
解:∵两圆内切于A,过外圆直径AB的一端B引外圆的弦BD与内圆切于C点,
∴OC∥AD,∴△BOC∽△BAD,∴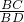 =
=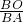 ,
,
设大圆半径为R,小圆为r
则有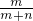 =
= ,①
,①
在Rt△OCB中,r2+m2=(2R-r)2②,
将①②两式组成方程组,解得:R=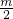 ,r=
,r=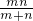 .
.
答:大圆半径为R=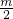 ,小圆半径为r=
,小圆半径为r=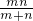 .
.
分析:根据两圆内切于A,过外圆直径AB的一端B引外圆的弦BD与内圆切于C点,求证△BOC∽△BAD,利用其对应边成比例,再设大圆半径为R,小圆为r,得出①②两式,解方程即可求出两圆半径的长.
点评:此题考查学生对相似三角形的判定与性质和勾股定理的理解和掌握,此题的关键是解关于两圆半径的方程,这是此题的难点.
∴OC∥AD,∴△BOC∽△BAD,∴
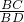 =
=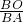 ,
,设大圆半径为R,小圆为r
则有
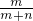 =
= ,①
,①在Rt△OCB中,r2+m2=(2R-r)2②,
将①②两式组成方程组,解得:R=
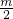 ,r=
,r=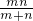 .
.答:大圆半径为R=
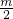 ,小圆半径为r=
,小圆半径为r=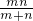 .
.分析:根据两圆内切于A,过外圆直径AB的一端B引外圆的弦BD与内圆切于C点,求证△BOC∽△BAD,利用其对应边成比例,再设大圆半径为R,小圆为r,得出①②两式,解方程即可求出两圆半径的长.
点评:此题考查学生对相似三角形的判定与性质和勾股定理的理解和掌握,此题的关键是解关于两圆半径的方程,这是此题的难点.

练习册系列答案
 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目
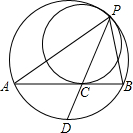 已知;如图,两圆内切于点P,大圆的弦AB切小圆于点C,PC的延长线交大圆于点D.
已知;如图,两圆内切于点P,大圆的弦AB切小圆于点C,PC的延长线交大圆于点D.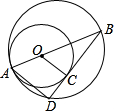 如图,已知两圆内切于A,过外圆直径AB的一端B引外圆的弦BD与内圆切于C点,若BC=m,CD=n,求两圆半径的长.
如图,已知两圆内切于A,过外圆直径AB的一端B引外圆的弦BD与内圆切于C点,若BC=m,CD=n,求两圆半径的长.
