题目内容
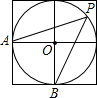如图，大正方形由4个相同的小正方形拼成，A、B、O是小正方形顶点，P是大正方形的内切圆⊙O上的点，且位于右上方的小正方形内．那么∠APB=
- A.30°
- B.45°
- C.60°
- D.90°
B
分析：根据圆周角定理在同圆与等圆中同弧与等弧所对圆周角是圆心角的一半，即可得出答案．
解答：∵∠AOB=90°，∠AOB与∠APB对着
，
∴∠APB=45°．
故选B．
点评：此题主要考查了圆周角定理的性质，圆周角定理的考查是初中阶段重点内容同学们应熟练掌握．
分析：根据圆周角定理在同圆与等圆中同弧与等弧所对圆周角是圆心角的一半，即可得出答案．
解答：∵∠AOB=90°，∠AOB与∠APB对着
，∴∠APB=45°．
故选B．
点评：此题主要考查了圆周角定理的性质，圆周角定理的考查是初中阶段重点内容同学们应熟练掌握．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
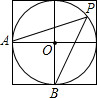如图，大正方形由4个相同的小正方形拼成，A、B、O是小正方形顶点，P是大正方形的内切圆⊙O上的点，且位于右上方的小正方形内．那么∠APB=（ ）| A、30° | B、45° | C、60° | D、90° |
如图，大正方形由9个相同的小正方形组成，三个小正方形已涂黑．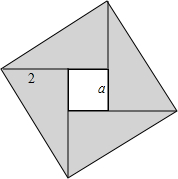
如图，大正方形由四个完全相同的直角三角形和中间的小正方形构成，已知直角三角形较短的直角边为2，小正方形边长为a．
如图，大正方形由9个相同的小正方形组成，三个小正方形已涂黑．