题目内容
在同一坐标系中，画出函数y=-x2和y=-x2+1的图象，根据图象回答：
（1）抛物线y=-x2+1经过怎样的平移得到抛物线y=-x2
（2）对于函数y=-x2+1：
①当x为何值时，y随x的增大而减小？
②当x为何值时，函数y有最大值？最大值是多少？
③求y=-x2+1的图象与x轴、y轴的交点坐标．
（1）抛物线y=-x2+1经过怎样的平移得到抛物线y=-x2
（2）对于函数y=-x2+1：
①当x为何值时，y随x的增大而减小？
②当x为何值时，函数y有最大值？最大值是多少？
③求y=-x2+1的图象与x轴、y轴的交点坐标．
分析：（1）作出图象即可得到平移方向和单位；
（2）利用二次函数的性质求解即可；
（2）利用二次函数的性质求解即可；
解答：解：图象为：
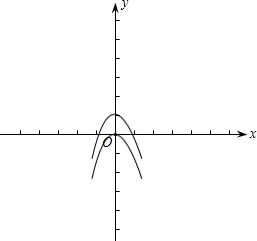
（1）抛物线y=-x2+1向下平移一个单位得到抛物线y=-x2；
（2）对于函数y=-x2+1：
①当x＜0时，y随x的增大而减小；
②当x=0时，函数y有最大值，最大值是1；
③令y=-x2+1=0，
解得x=±1，
∴与x轴的交点坐标为（-1，0）（1，0），
令x=0，解得：y=1，
∴与y轴交与（0，1）．
（1）抛物线y=-x2+1向下平移一个单位得到抛物线y=-x2；
（2）对于函数y=-x2+1：
①当x＜0时，y随x的增大而减小；
②当x=0时，函数y有最大值，最大值是1；
③令y=-x2+1=0，
解得x=±1，
∴与x轴的交点坐标为（-1，0）（1，0），
令x=0，解得：y=1，
∴与y轴交与（0，1）．
点评：本题考查了二次函数的性质，做出图象后即可得到平移的单位和方向．
练习册系列答案
相关题目
在同一坐标系中，画出函数y=kx+b与y=
（k＞0，b＞0）的图象，则下列说法正确的是（ ）
| k |
| x |
| A、这两个函数的图象在第一、三象限有交点 |
| B、这两个函数的图象在第二、四象限有交点 |
| C、这两个函数的图象无论在哪个象限都不可能有交点 |
| D、这两个函数的图象是否有交点无法确定 |
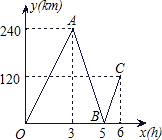行驶的时间为x（h），两船之间的距离为y（km），图中的折线表示y与x之间的函数关系．