题目内容
反比例函数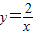 的图象与坐标轴有 个交点,图象在 象限,当x>0时函数值y随x的增大而 .
的图象与坐标轴有 个交点,图象在 象限,当x>0时函数值y随x的增大而 .
【答案】分析:根据反比例函数的性质进行解答即可.
解答:解:∵反比例函数y=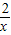 中x≠0,y≠0,
中x≠0,y≠0,
∴此函数的图象与坐标轴没有交点;
∵k=2>0,
∴此函数的图象在一、三象限;
∵k>0,
∴此函数在每一象限内y随x的增大而减小,
∴当x>0时函数值y随x的增大而减小.
故答案为:0;一、三;减小.
点评:本题考查的是反比例函数的性质,即
(1)反比例函数y=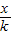 (k≠0)的图象是双曲线;
(k≠0)的图象是双曲线;
(2)当k>0,双曲线的两支分别位于第一、第三象限,在每一象限内y随x的增大而减小;
(3)当k<0,双曲线的两支分别位于第二、第四象限,在每一象限内y随x的增大而增大.
解答:解:∵反比例函数y=
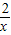 中x≠0,y≠0,
中x≠0,y≠0,∴此函数的图象与坐标轴没有交点;
∵k=2>0,
∴此函数的图象在一、三象限;
∵k>0,
∴此函数在每一象限内y随x的增大而减小,
∴当x>0时函数值y随x的增大而减小.
故答案为:0;一、三;减小.
点评:本题考查的是反比例函数的性质,即
(1)反比例函数y=
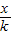 (k≠0)的图象是双曲线;
(k≠0)的图象是双曲线;(2)当k>0,双曲线的两支分别位于第一、第三象限,在每一象限内y随x的增大而减小;
(3)当k<0,双曲线的两支分别位于第二、第四象限,在每一象限内y随x的增大而增大.

练习册系列答案
相关题目

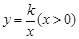 的图象与边BC交于点F。
的图象与边BC交于点F。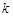 的值:
的值: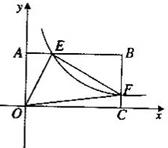
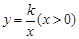 的图象与边BC交于点F。
的图象与边BC交于点F。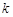 的值:
的值:
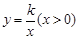 的图象与边BC交于点F。
的图象与边BC交于点F。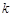 的值:
的值:
 的图象与边BC交于点F.
的图象与边BC交于点F.
 .且
.且 ,求k的值.
,求k的值.