ЬтФПФкШн
ЁОЬтФПЁПШєБфСПzЪЧБфСПyЕФКЏЪ§ЃЌЭЌЪББфСПyЪЧБфСПxЕФКЏЪ§ЃЌФЧУДЮвУЧАбБфСПzНазіБфСПxЕФЁАЕќДњКЏЪ§ЁБ.
Р§ШчЃКz2y3ЃЌyx1ЃЌдђz2x132x1ЃЌФЧУДz2x1ОЭЪЧzгыxжЎМфЕФЁАЕќДњКЏЪ§ЁБНтЮіЪН.
ЃЈ1ЃЉЕБ2006x2020ЪБЃЌzy2ЃЌ![]() ЃЌЧыЧѓГіzгыxжЎМфЕФЁАЕќДњКЏЪ§ЁБЕФНтЮіЪНМАzЕФзюаЁжЕЃЛ
ЃЌЧыЧѓГіzгыxжЎМфЕФЁАЕќДњКЏЪ§ЁБЕФНтЮіЪНМАzЕФзюаЁжЕЃЛ
ЃЈ2ЃЉШєz2yaЃЌyax24axba0ЃЌЕБ1x3ЪБЃЌЁАЕќДњКЏЪ§ЁБzЕФШЁжЕЗЖЮЇЮЊ1z17ЃЌЧѓaКЭbЕФжЕЃЛ
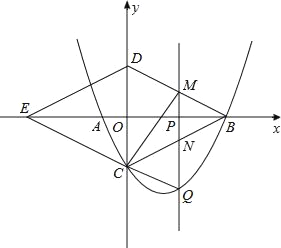
ЃЈ3ЃЉвбжЊвЛДЮКЏЪ§yax1ОЙ§Еу1,2ЃЌzay2b2ycb4ЃЈЦфжаaЁЂbЁЂcОљЮЊГЃЪ§ЃЉЃЌДЯУїЕФФуУЧвЛЖЈжЊЕРЁАЕќДњКЏЪ§ЁБzЪЧxЕФЖўДЮКЏЪ§ЃЌШєx1ЁЂx2ЃЈx1x2ЃЉЪЧЁАЕќДњКЏЪ§ЁБz3ЕФСНИіИљЃЌЕуx3,2ЪЧЁАЕќДњКЏЪ§ЁБzЕФЖЅЕуЃЌЖјЧвx1ЁЂx2ЁЂx3ЛЙЪЧвЛИіжБНЧШ§НЧаЮЕФШ§ЬѕБпГЄЃЌЧыЦЦНтЁАЕќДњКЏЪ§ЁБzЙигкxЕФКЏЪ§НтЮіЪН.
ЁОД№АИЁПЃЈ1ЃЉz= -![]() x+6ЃЛ-1004ЃЛЃЈ2ЃЉ
x+6ЃЛ-1004ЃЛЃЈ2ЃЉ Лђ
Лђ ЃЛЃЈ3ЃЉ
ЃЛЃЈ3ЃЉ![]()
ЁОНтЮіЁП
ЃЈ1ЃЉАб![]() ДњШыzy2жаЛЏМђМДПЩЕУГіД№АИЃЛ
ДњШыzy2жаЛЏМђМДПЩЕУГіД№АИЃЛ
ЃЈ2ЃЉАбyax24axba0ДњШыz2yaећРэЕУz=2a(x-2) 2-7a+2b,дйЗжСНжжЧщПіЬжТлЃЌЗжБ№ЕУЗНГЬзщ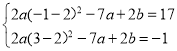 КЭ
КЭ ЃЌЧѓНтМДПЩЕУЃЛ
ЃЌЧѓНтМДПЩЕУЃЛ
ЃЈ3ЃЉАбЃЈ1ЃЌ2ЃЉДњШыy=ax+1НтЕУa=1ЃЌЕУГіy=x+1ЃЌдйНЋy=x+1ДњШыz=ay2+ЃЈb-2ЃЉy+c-b+4ЕУ![]() ЃЌИљОнЕуx3,2ЪЧЁАЕќДњКЏЪ§ЁБzЕФЖЅЕуЕУГі
ЃЌИљОнЕуx3,2ЪЧЁАЕќДњКЏЪ§ЁБzЕФЖЅЕуЕУГі![]()
![]() ЃЌдйИљОнЕБz=3ЪБЃЌ
ЃЌдйИљОнЕБz=3ЪБЃЌ ![]() НтЕУ
НтЕУ![]() ЃЌгжx1ЁЂx2ЁЂx3ЪЧвЛИіжБНЧШ§НЧаЮЕФШ§ЬѕБпГЄЕУ
ЃЌгжx1ЁЂx2ЁЂx3ЪЧвЛИіжБНЧШ§НЧаЮЕФШ§ЬѕБпГЄЕУ![]() ЃЌДњШыНтЕУb=-8,c=15,ДгЖјЕУНтЁЃ
ЃЌДњШыНтЕУb=-8,c=15,ДгЖјЕУНтЁЃ
НтЃКЃЈ1ЃЉАб![]() ДњШыzy2жаЕУЃК
ДњШыzy2жаЕУЃК
zЃЈ![]() ЃЉ2= -
ЃЉ2= -![]() x+6
x+6
Ёп-![]() ЃМ0ЃЌ
ЃМ0ЃЌ
ЁрzЫцзХxЕФдіДѓЖјМѕаЁЃЌ
Ёп2006 x2020 ЃЌ
ЁрЕБx=2020ЪБЃЌzгазюаЁжЕЃЌзюаЁжЕЮЊz= -![]() ЁС2020+6=-1004
ЁС2020+6=-1004
ЙЪД№АИЮЊЃКz= -![]() x+6ЃЛ-1004
x+6ЃЛ-1004
ЃЈ2ЃЉАбyax24axba0ДњШыz2yaЃЌЕУ
z2ЃЈax24axbЃЉa
=2ax28axbaЃЌ
=2a(x-2) 2-7a+2b
етЪЧвЛИіЖўДЮКЏЪ§ЃЌЭМЯѓЕФЖдГЦжсЪЧжБЯпx=2ЃЌ
ЕБaЃО0ЪБЃЌгЩКЏЪ§ЭМЯѓЕФаджЪПЩЕУx=-1ЪБЃЌz=17;x=3ЪБЃЌz=-1;
Ёр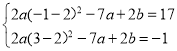
НтЕУ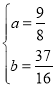
ЕБaЃМ0ЪБЃЌгЩКЏЪ§ЭМЯѓЕФаджЪПЩЕУx=-1ЪБЃЌz=-1;x=3ЪБЃЌz=17;
Ёр
НтЕУ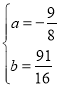
злЩЯЃЌ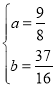 Лђ
Лђ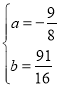
ЃЈ3ЃЉАбЃЈ1ЃЌ2ЃЉДњШыy=ax+1ЕУa+1=2
НтЕУa=1
Ёрy=x+1
Абy=x+1ДњШыz=ay2+ЃЈb-2ЃЉy+c-b+4ВЂећРэЕУ
![]()
ЁпЕуx3,2ЪЧЁАЕќДњКЏЪ§ЁБzЕФЖЅЕу,
![]()
ећРэЕУ![]()
ЕБz=3ЪБЃЌ ![]()
НтЕУ![]()
гжЁпx1x2
Ёрx1 x3x2
гжЁпx1ЁЂx2ЁЂx3ЛЙЪЧвЛИіжБНЧШ§НЧаЮЕФШ§ЬѕБпГЄ
Ёр![]()
МД![]()
НтЕУ![]()
Ёр![]()
Аб![]() ДњШы
ДњШы![]()
НтЕУc=15
Ёр![]()
![]()
ЙЪД№АИЮЊЃК![]()