题目内容
【题目】如图,已知DC∥FP,∠1=∠2,∠FED=28°,∠AGF=80°,FH平分∠EFG. 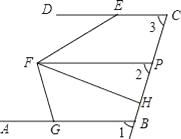
(1)说明:DC∥AB;
(2)求∠PFH的度数.
【答案】
(1)解:∵DC∥FP,
∴∠3=∠2,
又∵∠1=∠2,
∴∠3=∠1,
∴DC∥AB;
(2)解:∵DC∥FP,DC∥AB,∠DEF=28°,
∴∠DEF=∠EFP=28°,AB∥FP,
又∵∠AGF=80°,
∴∠AGF=∠GFP=80°,
∴∠GFE=∠GFP+∠EFP=80°+28°=108°,
又∵FH平分∠EFG,
∴∠GFH= ![]() ∠GFE=54°,
∠GFE=54°,
∴∠PFH=∠GFP﹣∠GFH=80°﹣54°=26°
【解析】(1)由DC∥FP知∠3=∠2=∠1,可得;(2)由(1)利用平行线的判定得到AB∥PF∥CD,根据平行线的性质得到∠AGF=∠GFP,∠DEF=∠EFP,然后利用已知条件即可求出∠PFH的度数.
【考点精析】认真审题,首先需要了解平行线的判定与性质(由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质).

练习册系列答案
相关题目
【题目】星光橱具店购进电饭煲和电压锅两种电器进行销售,其进价与售价如下表:
进价(元/台) | 售价(元/台) | |
电饭煲 | 200 | 250 |
电压锅 | 160 | 200 |
(1)一季度,橱具店购进这两种电器共30台,用去了5600元,并且全部售完,问橱具店在该买卖中赚了多少钱?
(2)为了满足市场需求,二季度橱具店决定用不超过9000元的资金采购电饭煲和电压锅共50台,且电饭煲的数量不少于电压锅的 ![]() ,橱具店有哪几种进货方案?并说明理由.
,橱具店有哪几种进货方案?并说明理由.
(3)在(2)的条件下,直接写出橱具店赚钱最多的进货方案.