题目内容
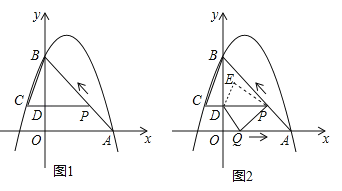
【题目】已知抛物线y1=ax2+bx+c(a≠0,a≠c)过点A(1,0),顶点为B,且抛物线不经过第三象限.
(1)使用a、c表示b;
(2)判断点B所在象限,并说明理由;
(3)若直线y2=2x+m经过点B,且交抛物线于另一点C(![]() ,b+8),求当x≥1时,y1的取值范围.
,b+8),求当x≥1时,y1的取值范围.
【答案】(1)b=-a-c;(2)第四象限,理由见解析;(3)y1≥-2.
【解析】
试题分析:此题主要考查了二次函数的综合应用以及根与系数的关系和一次函数与二次函数交点问题等知识,根据数形结合得出是解题关键.
(1)抛物线经过A(1,0),把点代入函数即可得到b=-a-c;
(2)判断点在哪个象限,需要根据题意画图,由条件:图象不经过第三象限就可以推出开口向上,a>0,只需要知道抛物线与x轴有几个交点即可解决,判断与x轴有两个交点,一个可以考虑△,由△就可以判断出与x轴有两个交点,所以在第四象限;或者直接用公式法(或十字相乘法)算出,由两个不同的解x1=1,x2=![]() ,(a≠c),进而得出点B所在象限;
,(a≠c),进而得出点B所在象限;
(3)当x≥1时,y1的取值范围,只要把图象画出来就清晰了,难点在于要观察出C(![]() ,b+8)是抛物线与x轴的另一个交点,理由是x1=1,x2=
,b+8)是抛物线与x轴的另一个交点,理由是x1=1,x2=![]() ,(a≠c),由这里可以发现,b+8=0,b=-8,a+c=8,还可以发现C在A的右侧;可以确定直线经过B、C两点,看图象可以得到,x≥1时,y1大于等于最小值,此时算出二次函数最小值即可,即求出
,(a≠c),由这里可以发现,b+8=0,b=-8,a+c=8,还可以发现C在A的右侧;可以确定直线经过B、C两点,看图象可以得到,x≥1时,y1大于等于最小值,此时算出二次函数最小值即可,即求出![]() 即可,已经知道b=-8,a+c=8,算出a,c即可,即可得出y1的取值范围.
即可,已经知道b=-8,a+c=8,算出a,c即可,即可得出y1的取值范围.
试题解析:(1)∵抛物线y1=ax2+bx+c(a≠0,a≠c),经过A(1,0),
把点代入函数即可得到:b=-a-c;
(2)B在第四象限.
理由如下:
∵抛物线y1=ax2+bx+c(a≠0,a≠c)过点A(1,0),
∴x1=1,x2=![]() ,a≠c,
,a≠c,
所以抛物线与x轴有两个交点,
又因为抛物线不经过第三象限,
所以a>0,且顶点在第四象限;
(3)∵C(![]() ,b+8),且在抛物线上,
,b+8),且在抛物线上,
∴b+8=0,∴b=-8,
∵a+c=-b,
∴a+c=8,
把B、C两点代入直线解析式易得:c-a=4,
即![]() ,
,
解得:![]() ,
,
如图所示,C在A的右侧,
∴当x≥1时,y1≥![]() =-2.
=-2.

【题目】某蔬菜经营户从蔬菜批发市场批发蔬菜进行零售,部分蔬菜批发价格与零售价格如表:
蔬菜品种 | 西红柿 | 青椒 | 西兰花 | 豆角 |
批发价(元/㎏) | 3.6 | 5.4 | 8 | 4.8 |
零售价(元/㎏) | 5.4 | 8.4 | 14 | 7.6 |
请解答下列问题:
(1)第一天,该经营户批发西红柿和西兰花两种蔬菜共300㎏,用去了1520元钱,这两种蔬菜当天全部售完一共赚了多少元钱?
(2)第二天,该经营户用1520元仍然批发西红柿和西兰花,要想当天全部售完后所赚钱数不少于1050元,则该经营户最多能批发西红柿多少㎏?