题目内容

求证：顺次连接矩形四边中点所得的四边形是菱形．

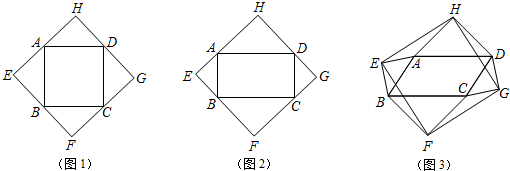
已知：如图，E、F、G、H分别为矩形ABCD四边的中点．
求证：四边形EFGH为菱形．
证明：连接AC、BD，
在△ABD中，
∵AH=HD，AE=EB
∴EH= $\text{[math]}$ BD，同理FG= $\text{[math]}$ BD，HG= $\text{[math]}$ AC，EF= $\text{[math]}$ AC，
又∵在矩形ABCD中，AC=BD，
∴EH=HG=GF=FE，
∴四边形EFGH为菱形．
分析：因为题中给出的条件是中点，所以可利用三角形中位线性质，以及矩形对角线相等去证明四条边都相等，从而说明是一个菱形．
点评：菱形的判别方法是说明一个四边形为菱形的理论依据，常用三种方法：①定义，②四边相等，③对角线互相垂直平分．

练习册系列答案

古诗文高效导学系列答案

古诗文夯基与积累系列答案

古诗文系统化教与学系列答案

课外古诗文阅读系列答案

初中课外文言文延边大学出版社系列答案

海豚图书课外现代文阅读系列答案

初中生必做的阅读理解与完形填空系列答案

DIY现代文阅读满分特训100篇系列答案

文言文课内外巩固与拓展系列答案

文言文扩展阅读系列答案

相关题目

以四边形ABCD的边AB、BC、CD、DA为斜边分别向外侧作等腰直角三角形，直角顶点分别为E、F、G、H，顺次连接这四个点，得四边形EFGH．
（1）如图1，当四边形ABCD为正方形时，我们发现四边形EFGH是正方形；如图2，当四边形ABCD为矩形时，请判断：四边形EFGH的形状（不要求证明）；
（2）如图3，当四边形ABCD为一般平行四边形时，设∠ADC=α（0°＜α＜90°），
①试用含α的代数式表示∠HAE；
②求证：HE=HG；
③四边形EFGH是什么四边形？并说明理由．

（2011•舟山）以四边形ABCD的边AB、BC、CD、DA为斜边分别向外侧作等腰直角三角形，直角顶点分别为E、F、G、H，顺次连接这四个点，得四边形EFGH．
（1）如图1，当四边形ABCD为正方形时，我们发现四边形EFGH是正方形；如图2，当四边形ABCD为矩形时，请判断：四边形EFGH的形状（不要求证明）；
（2）如图3，当四边形ABCD为一般平行四边形时，设∠ADC=α（0°＜α＜90°），
①试用含α的代数式表示∠HAE；
②求证：HE=HG；
③四边形EFGH是什么四边形？并说明理由．

（2011•舟山）以四边形ABCD的边AB、BC、CD、DA为斜边分别向外侧作等腰直角三角形，直角顶点分别为E、F、G、H，顺次连接这四个点，得四边形EFGH．
（1）如图1，当四边形ABCD为正方形时，我们发现四边形EFGH是正方形；如图2，当四边形ABCD为矩形时，请判断：四边形EFGH的形状（不要求证明）；
（2）如图3，当四边形ABCD为一般平行四边形时，设∠ADC=α（0°＜α＜90°），
①试用含α的代数式表示∠HAE；
②求证：HE=HG；
③四边形EFGH是什么四边形？并说明理由．

以四边形ABCD的边AB、BC、CD、DA为斜边分别向外侧作等腰直角三角形，直角顶点分别为E、F、G、H，顺次连接这四个点，得四边形EFGH。
（1）如图1，当四边形ABCD为正方形时，我们发现四边形EFGH是正方形；如图2，当四边形ABCD为矩形时，请判断：四边形EFGH的形状（不要求证明）；
（2）如图3，当四边形ABCD为一般平行四边形时，设∠ADC=α（0°＜α＜90°），
①试用含α的代数式表示∠HAE；
②求证：HE=HG；
③四边形EFGH是什么四边形？并说明理由。

以四边形ABCD的边AB、BC、CD、DA为斜边分别向外侧作等腰直角三角形，直角顶点分别为E、F、G、H，顺次连接这四个点，得四边形EFGH．

（1）如图1，当四边形ABCD为正方形时，我们发现四边形EFGH是正方形；如图2，当四边形ABCD为矩形时，请判断：四边形EFGH的形状（不要求证明）；

（2）如图3，当四边形ABCD为一般平行四边形时，设∠ADC=α（0°＜α＜90°），

①试用含α的代数式表示∠HAE；

②求证：HE=HG；

③四边形EFGH是什么四边形？并说明理由．