题目内容
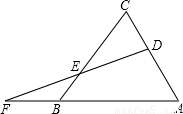
(2003•绵阳)已知:如图,D为△ABC的边AC上一点,F为AB延长线上一点,DF交BC于E.(1)若E是DF的中点,CD=BF,试判定△ABC的形状.
(2)若AC•DE=AB•EF,证明:CD=BF.
【答案】分析:(1)根据E是中点和CD=BF可以想到,△FBE与另一个三角形全等,所以过D作DG∥AB,这样△FBE≌△DGE,所以FB、GD、CD都相等∠C=∠DGC=∠ABC,所以三角形是等腰三角形;
(2)先把乘积式转化成比例式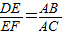 ,所以需要过D作DG∥AB,再利用平行得
,所以需要过D作DG∥AB,再利用平行得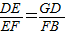 ,而由于平行还可以得到△ABC∽△DGC,得到
,而由于平行还可以得到△ABC∽△DGC,得到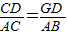 ,通过比例转化和等量代换即可得到CD=BF.
,通过比例转化和等量代换即可得到CD=BF.
解答: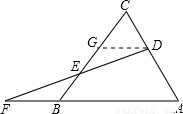 (1)解:过D作DG∥AB交BC于G,
(1)解:过D作DG∥AB交BC于G,
∴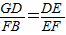 ,∠CGD=∠ABC
,∠CGD=∠ABC
∵E是DF的中点,
∴DE=EF
∴GD=FB
又∵CD=FB,∴CD=GD
∴∠C=∠CGD
∴∠C=∠ABC
所以△ABC是等腰三角形.
(2)证明:过D作DG∥AB交BC于G,
∴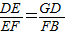 ,
,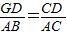
∴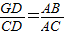
又∵AC•DE=AB•EF
∴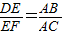
∴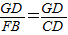
∴CD=BF.
点评:本题旨在考查通过作辅助线,把相关的两个量通过中间的一个量代换,从而使问题得以解决.
(2)先把乘积式转化成比例式
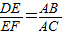 ,所以需要过D作DG∥AB,再利用平行得
,所以需要过D作DG∥AB,再利用平行得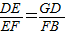 ,而由于平行还可以得到△ABC∽△DGC,得到
,而由于平行还可以得到△ABC∽△DGC,得到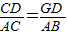 ,通过比例转化和等量代换即可得到CD=BF.
,通过比例转化和等量代换即可得到CD=BF.解答:
 (1)解:过D作DG∥AB交BC于G,
(1)解:过D作DG∥AB交BC于G,∴
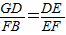 ,∠CGD=∠ABC
,∠CGD=∠ABC∵E是DF的中点,
∴DE=EF
∴GD=FB
又∵CD=FB,∴CD=GD
∴∠C=∠CGD
∴∠C=∠ABC
所以△ABC是等腰三角形.
(2)证明:过D作DG∥AB交BC于G,
∴
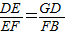 ,
,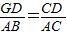
∴
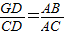
又∵AC•DE=AB•EF
∴
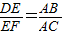
∴
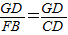
∴CD=BF.
点评:本题旨在考查通过作辅助线,把相关的两个量通过中间的一个量代换,从而使问题得以解决.

练习册系列答案
相关题目
 ,②DE⊥AB,③AF=DF.
,②DE⊥AB,③AF=DF.