题目内容

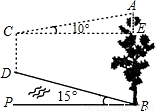
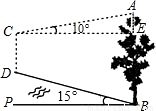
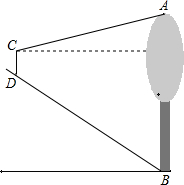如图，山脚下有一棵树AB，小强从点B沿山坡向上走50米到达点D，用高为1.5米的测解仪CD测得树顶的仰角为10°，已知山坡的坡角为45°，求AB的高（精确到0.1米，已知sin10°=0.17； cos10°=0.98； tan10°=0.18；sin15°=0.26； cos15°=0.97；  tan15°=0.27）
分析：由已知可得BD=50m，CD∥AB．要求AB的长可以延长CD交水平面与点F．则AB=AE+BE=AE+CD+DF，问题转化为求DF、AE，转化为解直角三角形．
解答：解：延长CD交PB于F，则DF⊥PB．
则DF=BD•sin45°=50×
2
2
≈35.4
CE=BF=BD•cos45°=50×
2
2
≈35.4
AE=CE•tan10°≈35.4×0.18≈6.4．
AB=AE+CD+DF=6.4+1.5+35.4=43.3．
答：树高约为43.3米．
点评：本题考查了解直角三角形的应用，解决梯形的问题可以通过作高线转化为解直角三角形和矩形的问题．
练习册系列答案
相关题目
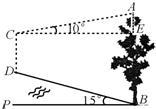24、如图，山脚下有一棵树AB，小华从点B沿山坡向上走50米到达点D，用高为1.5米的测角仪CD测得树顶的仰角为10°，已知山坡的坡角为15°，求树AB的高．（精确到0.1米）
（已知sin10°≈0.17，cos10°≈0.98，tan10°≈0.18，sin15°≈0.26，cos15°≈0.97，tan15°≈0.27．）
如图，山脚下有一棵树AB，小华从点B沿山坡向上走50米到达点D，用高为1.5米的测角仪CD测得树顶的仰角为10°，已知山坡的坡角为15°，求树AB的高．（精确到0.1米）
（已知sin10°≈0.17，cos10°≈0.98，tan10°≈0.18，sin15°≈0.26，cos15°≈0.97，tan15°≈0.27．）
（2008•荆门）如图，山脚下有一棵树AB，小华从点B沿山坡向上走50米到达点D，用高为1.5米的测角仪CD测得树顶的仰角为10°，已知山坡的坡角为15°，求树AB的高．（精确到0.1米）
（已知sin10°≈0.17，cos10°≈0.98，tan10°≈0.18，sin15°≈0.26，cos15°≈0.97，tan15°≈0.27．）
（2008•荆门）如图，山脚下有一棵树AB，小华从点B沿山坡向上走50米到达点D，用高为1.5米的测角仪CD测得树顶的仰角为10°，已知山坡的坡角为15°，求树AB的高．（精确到0.1米）
（已知sin10°≈0.17，cos10°≈0.98，tan10°≈0.18，sin15°≈0.26，cos15°≈0.97，tan15°≈0.27．）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网