题目内容
（2004•沈阳）沈阳市某中学举办校园文化艺术节，小颖设计了同学们喜欢的图案《我的宝贝》．图案的一部分是以斜边长为12cm的等腰直角三角形的各边为直径作半圆（如图），则图中阴影部分的面积为（ ）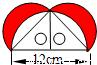
A．36πcm2
B．72πcm2
C．36cm2
D．72cm2
【答案】分析：阴影部分的面积等于中间等腰直角三角形的面积加上两个小半圆的面积，减去其中下面面积较大的半圆的面积．
解答：解：因为斜边长为12cm，则两直角边均为6
cm，
则两个小半圆的面积均为：
π（3
）2=9πcm2，
以斜边为直径的半圆的面积是
π（
）2=18πcm2，三角形的面积是36cm2，
因而阴影部分的面积=9π+9π+36-18π=36cm2．
故选C．
点评：图形中不规则图形的面积可以转化为一些不规则图形的面积的和或差的问题．
解答：解：因为斜边长为12cm，则两直角边均为6
cm，则两个小半圆的面积均为：
π（3）2=9πcm2，以斜边为直径的半圆的面积是
π（）2=18πcm2，三角形的面积是36cm2，因而阴影部分的面积=9π+9π+36-18π=36cm2．
故选C．
点评：图形中不规则图形的面积可以转化为一些不规则图形的面积的和或差的问题．
练习册系列答案
相关题目
（2004•沈阳）某市的A县和B县春季育苗，急需化肥分别为90吨和60吨．该市的C县和D县分别储存化肥100吨和50吨，全部调配给A县和B县，已知C、D两县运化肥到A、B两县的运费（元/吨）如下列表所示：
（1）设C县到A县的化肥为x吨，求总运费W（元）与x（吨）的函数关系式，并写出自变量x的取值范围；
（2）求最低总运费，并说明总运费最低时的运送方案．
| 目的地运费出发地 | C | D |
| A | 35 | 40 |
| B | 30 | 45 |
（2）求最低总运费，并说明总运费最低时的运送方案．
