题目内容
若一元二次方程的两根x1、x2满足下列关系:x1x2+x1+x2+2=0,x1x2-2x1-2x2+5=0.则这个一元二次方程是( )
分析:把x1x2+x1+x2+2=0,x1x2-2x1-2x2+5=0看作为x1+x2、x1x2的二元一次方程组,解得x1+x2=1,x1x2=-3,然后根据根与系数的关系写出满足条件的一元二次方程.
解答:解:∵x1x2+x1+x2+2=0,x1x2-2x1-2x2+5=0,
∴x1x2+(x1+x2)+2=0,x1x2-2(x1+x2)+5=0,
∴x1+x2=1,x1x2=-3,
∴以x1、x2为根的一元二次方程可为x2-x-3=0.
故选B.
∴x1x2+(x1+x2)+2=0,x1x2-2(x1+x2)+5=0,
∴x1+x2=1,x1x2=-3,
∴以x1、x2为根的一元二次方程可为x2-x-3=0.
故选B.
点评:本题考查了一元二次方程ax2+bx+c=0(a≠0)的根与系数的关系:x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-
,x1x2=
.
| b |
| a |
| c |
| a |

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
 的两根是等腰△ABC的两边,则△ABC的周长为_________。
的两根是等腰△ABC的两边,则△ABC的周长为_________。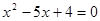 的两根是等腰△ABC的两边,则△ABC的周长为_________。
的两根是等腰△ABC的两边,则△ABC的周长为_________。