题目内容
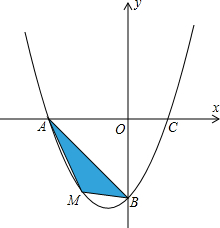
已知抛物线y=ax2+bx-4的图象与x相交于A、B(点A在B的左边),与y轴相交于C,抛物线过点A(-1,0)且OB=OC.P是线段BC上的一个动点,过P作直线PE⊥ x轴于E,交抛物线于F.
x轴于E,交抛物线于F.
(1)求抛物线的解析式;
(2)若△BPE与△BPF的两面积之比为2:3时,求E点的坐标;
(3)设OE=t,△CPE的面积为S,试求出S与t的函数关系式;当t为何值时,S有最大值,并求出最大值;
(4)在(3)中,当S取得最大值时,在抛物线上求点Q,使得△QEC是以EC为底边的等腰三角形,求Q的坐标.
 x轴于E,交抛物线于F.
x轴于E,交抛物线于F.(1)求抛物线的解析式;
(2)若△BPE与△BPF的两面积之比为2:3时,求E点的坐标;
(3)设OE=t,△CPE的面积为S,试求出S与t的函数关系式;当t为何值时,S有最大值,并求出最大值;
(4)在(3)中,当S取得最大值时,在抛物线上求点Q,使得△QEC是以EC为底边的等腰三角形,求Q的坐标.
(1)易知:C(0,-4),即OC=4;
故OB=OC=4,B(4,0);
将A(-1,0),B(4,0)代入抛物线的解析式中,得:
,
解得
;
故抛物线的解析式为:y=x2-3x-4.
(2)设E(x,0)(0<x<4),易知直线BC:y=x-4,则P(x,x-4),F(x,x2-3x-4);
故PE=4-x,PF=(x-4)-(x2-3x-4)=-x2+4x;
①若S△PBE:S△PBF=2:3,
则PE:PF=2:3,
即:
=
,
解得x=
,x=4(舍去),
②若S△PBE:S△PBF=3:2,则PE:PF=3:2,
即:
=
,
解得x=
;x=4(舍去)
综上所述,E点的坐标为:E(
,0)或(
,0).
(3)若OE=t,则(t,0);
由(2)知:PE=4-t,则有:
S△CPE=-
t2+2t(0≤t≤4);
当t=2时,S取得最大值,最大值为2.
(4)设线段CE的中点为M,即M(1,-2);
若△QCE是以EC为底边的等腰三角形,那么点Q必为线段CE的垂直平分线与抛物线的交点;
由于E(2,0)、C(0,4),
易知直线EC:y=2x-4;
所以设:直线QM:y=-
x+h,
代入M点坐标得:-
+h=-2,
即h=-
;
故直线QM:y=-
x-
,联立抛物线的解析式可得:
,
解得
,
;
故Q1(
,
),Q2(
,
).
故OB=OC=4,B(4,0);
将A(-1,0),B(4,0)代入抛物线的解析式中,得:
|
解得
|
故抛物线的解析式为:y=x2-3x-4.
(2)设E(x,0)(0<x<4),易知直线BC:y=x-4,则P(x,x-4),F(x,x2-3x-4);
故PE=4-x,PF=(x-4)-(x2-3x-4)=-x2+4x;
①若S△PBE:S△PBF=2:3,
则PE:PF=2:3,
即:
| 4-x |
| -x2+4x |
| 2 |
| 3 |
解得x=
| 3 |
| 2 |
②若S△PBE:S△PBF=3:2,则PE:PF=3:2,
即:
| 4-x |
| -x2+4x |
| 3 |
| 2 |
解得x=
| 2 |
| 3 |
综上所述,E点的坐标为:E(
| 3 |
| 2 |
| 2 |
| 3 |
(3)若OE=t,则(t,0);
由(2)知:PE=4-t,则有:
S△CPE=-
| 1 |
| 2 |
当t=2时,S取得最大值,最大值为2.
(4)设线段CE的中点为M,即M(1,-2);
若△QCE是以EC为底边的等腰三角形,那么点Q必为线段CE的垂直平分线与抛物线的交点;
由于E(2,0)、C(0,4),
易知直线EC:y=2x-4;
所以设:直线QM:y=-
| 1 |
| 2 |
代入M点坐标得:-
| 1 |
| 2 |
即h=-
| 3 |
| 2 |
故直线QM:y=-
| 1 |
| 2 |
| 3 |
| 2 |
|
解得
|
|
故Q1(
5+
| ||
| 4 |
-17-
| ||
| 8 |
5-
| ||
| 4 |
-17+
| ||
| 8 |

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
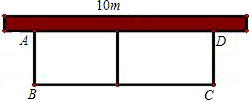 的长方形花园.设花园的宽AB为x米,面积为y米2
的长方形花园.设花园的宽AB为x米,面积为y米2 男生的抛球处A点坐标为(0,2),实心球在空中线路的最高点B点的坐标是(6,5).
男生的抛球处A点坐标为(0,2),实心球在空中线路的最高点B点的坐标是(6,5).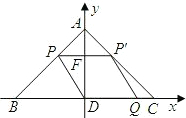 向作匀速运动,且满足四边形QDPP′是平行四边形.设平行四边形QDPP′的面积为y,DQ=x.
向作匀速运动,且满足四边形QDPP′是平行四边形.设平行四边形QDPP′的面积为y,DQ=x.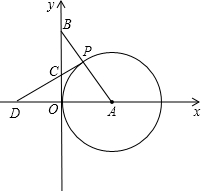 点P,过点P作⊙A的切线交y轴于点C,交x轴于点D.
点P,过点P作⊙A的切线交y轴于点C,交x轴于点D.