题目内容
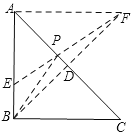
【题目】如图,E为等腰直角△ABC的边AB上的一点,要使AE=3,BE=1,P为AC上的动点,则PB+PE的最小值为____________.

【答案】5
【解析】试题分析:作点B关于AC的对称点F,构建直角三角形,根据最短路径可知:此时PB+PE的值最小,接下来要求出这个最小值,即求EF的长即可,因此要先求AF的长,证明△ADF≌△CDB,可以解决这个问题,从而得出EF=5,则PB+PE的最小值为5.
解:如图,过B作BD⊥AC,垂足为D,并截取DF=BD,连接EF交AC于P,连接PB、AF,则此时PB+PE的值最小,
∵△ABC是等腰直角三角形,
∴AB=CB,∠ABC=90°,AD=DC,
∴∠BAC=∠C=45°,
∵∠ADF=∠CDB,
∴△ADF≌△CDB,
∴AF=BC,∠FAD=∠C=45°,
∵AE=3,BE=1,
∴AB=BC=4,
∴AF=4,
∵∠BAF=∠BAC+∠FAD=45°+45°=90°,
∴由勾股定理得:EF=![]() =
=![]() =5,
=5,
∵AC是BF的垂直平分线,
∴BP=PF,
∴PB+PE=PF+PE=EF=5,
故答案为:5.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案
相关题目