题目内容
函数y=kx+b交x轴于(2,0),若其图象过二、四象限,则此函数关系式可以是 .
【答案】分析:先把(2,0)代入解析式,得2k+b=0,若其图象过二、四象限,则k<0,可取k=-1,得到b=2,这样就确定了一个满足条件的解析式.
解答:解:∵函数y=kx+b交x轴于(2,0),
∴2k+b=0,即b=-2k.
又∵函数图象y=kx+b过二、四象限,
∴k<0,则可取k=-1,得到b=2,
所以函数y=-x+2为满足条件的一个解析式.
故答案为y=-x+2.
点评:本题考查了一次函数y=kx+b(k≠0,k,b为常数)的性质.它的图象为直线,当k>0,图象经过第一,三象限,y随x的增大而大;当k<0,图象经过第二,四象限,y随x的增大而减小;当b>0,直线与y轴的交点在x轴上方;当b=0,直线经过坐标原点;当b<0,直线与y轴的交点在x轴下方.
解答:解:∵函数y=kx+b交x轴于(2,0),
∴2k+b=0,即b=-2k.
又∵函数图象y=kx+b过二、四象限,
∴k<0,则可取k=-1,得到b=2,
所以函数y=-x+2为满足条件的一个解析式.
故答案为y=-x+2.
点评:本题考查了一次函数y=kx+b(k≠0,k,b为常数)的性质.它的图象为直线,当k>0,图象经过第一,三象限,y随x的增大而大;当k<0,图象经过第二,四象限,y随x的增大而减小;当b>0,直线与y轴的交点在x轴上方;当b=0,直线经过坐标原点;当b<0,直线与y轴的交点在x轴下方.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
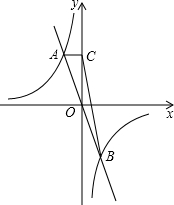 如图,函数y=-kx与
如图,函数y=-kx与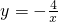 交于A、B两点,点A的坐标为(-1,m),AC垂直y轴于点C,则S△BCO=________.
交于A、B两点,点A的坐标为(-1,m),AC垂直y轴于点C,则S△BCO=________.