题目内容
【题目】如图，点A1 ， A2在射线OA上，B1在射线OB上，依次作A2B2∥A1B1 ， A3B2∥A2B1 ， A3B3∥A2B2 ， A4B3∥A3B2 ， …．若△A2B1B2和△A3B2B3的面积分别为1、9，则△A1007B1007A1008的面积是 ． 
【答案】32n﹣3
【解析】解：∵△A2B1B2和△A3B2B3的面积分别为1、9，A3B3∥A2B2 ， A3B2∥A2B1 ， ∴∠B1B2A2=∠B2B3A3 ， ∠A2B1B2=∠A3B2B3 ，
∴△A2B1B2∽△A3B2B3 ，
∴ 
= 
= 
= 
= 
，
∵A3B2∥A2B1 ，
∴△OA2B1∽△OA3B2 ，
∴ 
= = 
= ，
∴△OB1A2的面积为 
，△A1B1A2的面积为 ，△A2B2A3的面积为3，△A3B3A4的面积为27，…
∴△A1007B1007A1008的面积为 ×32（n﹣1）=32n﹣3 ，
所以答案是32n﹣3 ．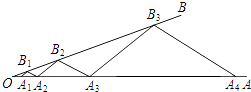 
【考点精析】掌握相似三角形的判定与性质是解答本题的根本，需要知道相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等）的比等于相似比；相似三角形周长的比等于相似比；相似三角形面积的比等于相似比的平方．
【题目】某校八年级在一次广播操比赛中，三个班的各项得分如下表：
服装统一 | 动作整齐 | 动作准确 | |
八（1）班 | 80 | 84 | 87 |
八（2）班 | 97 | 78 | 80 |
八（3）班 | 90 | 78 | 85 |
(1) 填空：根据表中提供的信息，在服装统一方面，三个班得分的平均数是_________；在动作准确方面最有优势的是_________班
(2) 如果服装统一、动作整齐、动作准确三个方面按20%、30%、50%的比例计算各班的得分，请通过计算说明哪个班的得分最高
