Question

如图，已知半圆O的直径AB=10，⊙O₁与半圆O内切干点C，与AB相切干点D，
（1）求证：CD平分∠ACB；
（2）若AC：CB=1：3，求△CDB的面积S_△CDB；
（3）设AC：CB=x（x＞0），⊙O₁的半径为y，请用含x的代数式表示y．

Answer 1

（1）证明：过点C作两圆外公切线MN；
∵AB与⊙O₁相切于点D，
∴∠MCD=∠ADC，∠MCA=∠ABC．
∵∠MCD=∠MCA+∠ACD，
∠ADC=∠ABC+∠BCD，
∴∠ACD=∠BCD，即CD平分∠ACB．

（2）解：∵AB是半圆O的直径，
∴∠ACB=90°，AC²+CB²=AB²，即AC²+CB²=100
已知AC：CB=1：3，
解得AC=，CB=3；
S_△ACB==

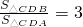
∴S_△CDB=．

（3）解：已知AC：CB=x，AC²+CB²=100解得
AC=，CB=，
过点C作CE⊥AB交AB于点E，S_△ABC=，
解得CE=（x＞0）．
连接OO₁并延长，则必过切点C，连O₁D，则O₁D⊥AB，
∴CE∥O₁D，
∴．
y=（x＞0）．
分析：（1）过点C作两圆外公切线MN，由角之间的等量关系，证明∠ACD=∠BCD，
（2）在Rt△ABC中，解得AC、BC的长，求出三角形面积，
（3）连接OO₁并延长，则必过切点C，连O₁D，求出AC、BC，由CE∥O₁D，列出x、y的关系式．
点评：本题主要考查两圆相切的性质，还考查的圆周角定理等知识点．