题目内容
某工厂生产一种机器的固定成本为5000元,且每生产100台需要投入2500元,对销售市场进行调查后,得知市场对此产品的需求量为每年500台,且销售收入可看作是函数y=500x-| 1 | 2 |
(1)分别写出当0≤x≤500及x>500时利润w与年产量x之间的函数关系式;
(2)请你运用函数知识,为该厂厂长设计一个最佳的生产计划,并求出由此计划获得的最大年利润是多少?
分析:(1)本题考查的是分段函数的有关知识.当0≤x≤500时,w=500x-
x2-(5000+25x);
当x>500时,w=500×500-
-5002;
(2)用配方法化简解析式,求出最大值.
| 1 |
| 2 |
当x>500时,w=500×500-
| 1 |
| 2 |
(2)用配方法化简解析式,求出最大值.
解答:解:(1)当0≤x≤500时,产品全部售出
∴W=500x-
x2-(5000+25x)
即W=-
x2+475x-5000(2分)
当x>500时,产品只能售出500台
∴W=500×500-
×5002-(5000+25x)
即,W=-25x+120000(4分)
(2)当0≤x≤500时,W=-
(x-475)2+107812.5(6分)
当x>500时,W=120000-25x<120000-25×500=107500(8分)
故当年产量为475台时取得最大利润,且最大利润为107812.5元,最佳生产计划475台.(10分)
∴W=500x-
| 1 |
| 2 |
即W=-
| 1 |
| 2 |
当x>500时,产品只能售出500台
∴W=500×500-
| 1 |
| 2 |
即,W=-25x+120000(4分)
(2)当0≤x≤500时,W=-
| 1 |
| 2 |
当x>500时,W=120000-25x<120000-25×500=107500(8分)
故当年产量为475台时取得最大利润,且最大利润为107812.5元,最佳生产计划475台.(10分)
点评:本题考查的是二次函数的实际应用,用配方法可求出最大值.

练习册系列答案
相关题目
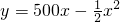 ,其中x是产品售出的数量,且0≤x≤500,已知此机器重要部件更新换代快,若造成积压,第二年无法卖出或无利可图.
,其中x是产品售出的数量,且0≤x≤500,已知此机器重要部件更新换代快,若造成积压,第二年无法卖出或无利可图.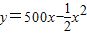 ,其中x是产品售出的数量,且0≤x≤500,已知此机器重要部件更新换代快,若造成积压,第二年无法卖出或无利可图.
,其中x是产品售出的数量,且0≤x≤500,已知此机器重要部件更新换代快,若造成积压,第二年无法卖出或无利可图.