题目内容
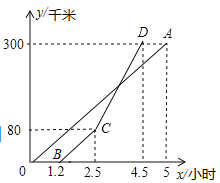
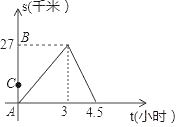
【题目】某电视台摄制组乘船往返于A码头和B码头进行拍摄，在A、B两码头间设置拍摄中心C．在往返过程中，假设船在A、B、C处均不停留，船离开B码头的距离s（千米）与航行的时间t（小时）之间的函数关系式如图所示．根据图象信息，解答下列问题：
（1）求船从B码头返回A码头时的速度及返回时s关于t的函数表达式．
（2）求水流的速度．
（3）若拍摄中心C设在离A码头12千米处，摄制组在拍摄中心分两组拍摄，其中一组乘橡皮艇漂流到B码头处，另一组同时乘船到达A码头后马上返回，求两摄制组相遇时离拍摄中心C的距离．
【答案】（1）s＝9t；（2）4.5千米/时；（3）12千米
【解析】
（1）根据题意，船从B码头返回A码头时的速度27÷3＝9千米/时，
设返回时s关于t的函数表达式为s＝kt，过（3，27），即可得出k＝9，进而求出s关于t的函数表达式为s＝9t （0≤t≤3）
（2）首先分别求出船由B到A的速度和由A到B的速度，再根据：顺水速﹣逆水速＝水速的2倍即可得出水流的速度；
（3）首先求出当船到达A地用时，再求出此时橡皮艇行至距C地的距离，设船从A返回追橡皮艇时间为x时，则可得出18x＝4.5x+12+6，解得x＝
，即可求出此时距C的距离．
解：（1）船从B码头返回A码头时的速度27÷3＝9千米/时，
设返回时s关于t的函数表达式为s＝kt，过（3，27）
∴k＝9
∴s关于t的函数表达式为s＝9t （0≤t≤3）
答：船从B码头返回A码头时的速度为9千米/时，返回时s关于t的函数表达式为：s＝9t．
（2）船由B到A的速度为：27÷3＝9千米/时，由A到B的速度为：27÷（4.5﹣3）＝18千米/时，
根据：顺水速﹣逆水速＝水速的2倍得：（18﹣9）÷2＝4.5千米/时，
故水流的速度为4.5千米/时；
（3）当船到达A地用时为：12÷9＝时，此时橡皮艇行至距C地4.5×＝6千米处，
设船从A返回追橡皮艇时间为x时，则：18x＝4.5x+12+6
解得：x＝
此时距C的距离为：4.5×（+）＝12千米．
答：两摄制组相遇时离拍摄中心C的距离为12千米．
